Functional Skills: Problems Involving Money
Problems Involving Money
There are several types of problems that you will encounter involving money – some are harder than others.
There are 5 skills that you need to learn for problems involving money.
Make sure you are happy with the following topics before continuing.
Skill 1: Converting between pounds (£) and pence (p)
Many questions require you to add and subtract values in both pounds (£) and pence (p), so you need to be able to switch between the two.
- To go from pounds to pence, multiply by 100
- To go from pence to pounds, divide by 100
Example: To convert £3.27 into pence, we multiply 3.27 by 100
So,
£3.27=327p
Example: To convert 47p into pounds, we divide 47 by 100
So,
47p =£0.47
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Skill 2: Rate of Pay
The rate of pay is the cost of something per unit of time, for example a phone call may cost 25p per minute or someone may get paid £11.70 per hour.
Often questions require you to combine a rate of pay with a fixed fee, or combine two different rates of pay.
Example: Sarah earns \textcolor{red}{£9.80} per hour and works \textcolor{limegreen}{30} hours in one week. She earned \textcolor{red}{£32.50} in tips.
How much did she earn in the week?
First calculate how much she earns from her hourly rate of pay: \textcolor{limegreen}{30}\times \textcolor{red}{£9.80}=£294
Then calculate her total earnings for the week: £294+\textcolor{red}{£32.50}=\textcolor{black}{£326.50}
Example: Stephen wants to re-tile his bathroom and also replace his shower.
A tiler charges \textcolor{red}{£24} per hour and says it will take \textcolor{limegreen}{11} hours work.
A plumber charges \textcolor{red}{£28.50} per hour and says it will take \textcolor{limegreen}{9} hours to fit the work.
How much will it cost Stephen in total to do both jobs?
Cost of re-tiling his bathroom: \textcolor{red}{£24} \times \textcolor{limegreen}{11}=£264
Cost of replacing his shower: \textcolor{red}{£28.50} \times \textcolor{limegreen}{9}=£256.50
Total Cost: £264+£256.50=\textcolor{black}{£520.50}
Skill 3: Discounts and Increases as Percentages
Often questions ask you to find the new price of an item after it has been increased or discounted by a certain percentage.
For LEVEL 1 you will only see discounts and increases given in multiples of 5\%, where as for LEVEL 2 you will need to work with all percentages.
You may need to re-visit percentage increase and percentage decrease to help you answer these types of questions.
Price Decrease
If a product’s price has been reduced by a percentage, we take this value away from 100\% and then convert this value into a decimal to then multiply it by the original price.
Example: A pair of trainers costs \textcolor{orange}{£45}. If there is a sale on which gives \textcolor{blue}{20\%} off the price, what will be the new price of the trainers?
100\% - 20\%=80\%=0.8New price of the trainers: \textcolor{orange}{£45}\times0.8=\textcolor{black}{£36}
Price Increase
If a product’s price has been increased by a percentage, we add this value to 100\% and then convert this value into a decimal to then multiply it by the original price.
Example: Lucy bought a house for \textcolor{orange}{£210000} last year, she has the house valued 1 year later and is told that the value of the house has increased by \textcolor{blue}{10\%}. Calculate the new value of the house.
100\%+10\%=110\%=1.1
New value of house: 1.1 \times \textcolor{orange}{£210000}=\textcolor{black}{£231000}
Note: Alternatively, we could have found what 10\% of £210000 was and then added this to the original value of the house.
Skill 4: Discounts as Fractions
You could also be asked to find the new price of an item after a discount in terms of a fraction has been applied.
You may need to re-visit fractions to help you answer these types of questions.
Example: A bike costs \textcolor{orange}{£330}. If there is a sale on which gives \textcolor{blue}{\dfrac{2}{5}} off the price, what will be the new price of the bike?
First, calculate \dfrac{2}{5} of the original price:
2 \div 5 \times \textcolor{orange}{£330} = £132
Then, subtract this from the original price of the bike:
\textcolor{orange}{£330} - £132 = \textcolor{black}{£198}
Skill 5: Percentage Profit
Percentage profit is the profit of selling an item as a percentage of the total costs involved.
\text{\textcolor{purple}{Profit}} = \text{\textcolor{blue}{Selling Price}} - \text{\textcolor{red}{Costs}}
\textcolor{limegreen}{\% \text{ Profit}}=\dfrac{\text{\textcolor{purple}{Profit}}}{\text{\textcolor{red}{Costs}}}\times100
Example: Gareth buys an old car for £1250, he then buys some replacement parts for £250. He sells the car on for £2100, calculate his percentage profit.
Profit =£2100-(£1250+£250)=£600
\% Profit =\dfrac{600}{1500}\times100=40\%
Functional Skills: Problems Involving Money Example Questions
Question 1: Convert 157p into pounds (£).
[1 mark]
To convert pence into pounds we need to divide by 100
157 \div 100=1.57
So,
157p = £1.57
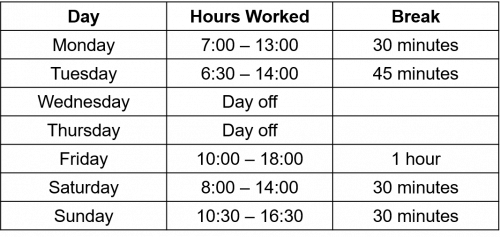
Question 2: Henry earns £10.20 Monday to Friday and £11.60 on weekends.
The table below shows his shifts for this week.
Henry’s breaks are not paid.
Work out how much Henry earns in the week.
[4 marks]
First we need to work out how many hours he works from Monday to Friday.
6+7.5+8=21.5 hours
Then subtract his breaks
21.5-(0.5+0.75+1)=19.25 hours
Now work out how many hours he worked during the weekend.
6+6=12 hours
Subtracting his breaks:
12-(0.5+0.5)=11 hours
Finally, calculate how much he earns during the whole week:
19.25 \times £10.20 + 11 \times £11.60=£323.95
Question 3: A shop is having a sale on all t-shirts of 25\%. Sam wants to buy a t-shirt, with an original price of £32.
Calculate the sale price of the t-shirt.
[2 marks]
100\%-25\%=75\%=0.75
£32\times0.75=£24
Question 4: Liam wants to book a hotel for a 7-night stay. The cost of the hotel for this stay is usually £480. An offer gives \dfrac{2}{15} off the usual price.
How much will the hotel cost Liam with the offer?
[2 marks]
Calculate \dfrac{2}{15} of the usual cost:
2 \div 15 \times £480 = £64
Then, subtract this from the usual cost:
£480 - £64 = £416
Question 5: Carla buys a house for £180000 and then spends £20000 on refurbishing the house.
She then sells it for £230000
Work out her percentage profit on the house to 1 decimal place.
[2 marks]
Profit =£230000-(£180000+£20000)=£30000
% Profit =\dfrac{30000}{200000}\times100=15.0\%
Specification Points Covered
L1.19 – Calculate discounts in multiples of 5% on amounts of money
L1.20 – Convert between units of length, weight, capacity, money and time, in the same system
L2.13 – Calculate amounts of money, compound interest, percentage increases, decreases and discounts including tax and simple budgeting
Functional Skills: Problems Involving Money Worksheet and Example Questions
Problems Involving Money L1
FS Level 1NewOfficial PFSProblems Involving Money L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.