Functional Skills: Decimals
Decimals
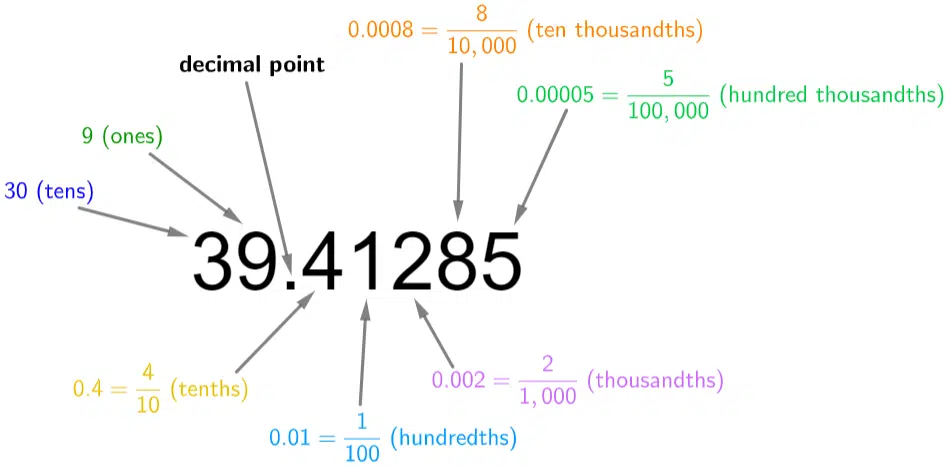
A decimal is any number with a decimal point. Decimals are numbers that lie between whole numbers, e.g. 90.2, 4.57 or 39.41285
There are 5 skills you need to learn for decimals, however they all use methods that you will have previously learned.
Make sure you are happy with the following topics before continuing.
Decimal Place Value
The digits after the decimal point also have values. The value decreases the further right you move away from the decimal point.
e.g. the number 39.41285 can be split up into:
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Skill 1: Adding Decimals
Adding decimals without a calculator uses the same column method as for whole numbers, you just have to make sure to line up the decimal points.
Example: Calculate 6.436 + 8.992
Use the column method for addition, like below:

Therefore,
6.436 + 8.992 = \textcolor{red}{15.428}
Skill 2: Subtracting Decimals
Subtracting decimals without a calculator uses the same column method as for whole numbers, you just have to make sure to line up the decimal points and add 0’s to the end of a number (if necessary) so that both numbers have the same number of decimal places.
Example: Calculate 567.63 - 92.478
Use the column method for subtraction like below, adding a 0 so that both numbers have 3 decimal places:

Therefore,
567.63 - 92.478 = \textcolor{red}{475.152}
Skill 3: Multiplying Decimals
To multiply decimals without a calculator, use the following steps:
Step 1: Convert the decimals to whole numbers by moving the decimal point to the right.
Step 2: Take note of how many decimal places that were moved in total.
Step 3: Complete the column method or grid method for multiplying without a calculator.
Step 4: Move the same number of decimal places back at the end. Now you have the final answer.
Example: Calculate 7.68 \times 2.5
The decimal point is moved one time on 2.5 to make it 25 and two times on 7.68 to make it 768. So, 3 decimal places were moved altogether.
Now, use the column method as seen below (or the grid method):
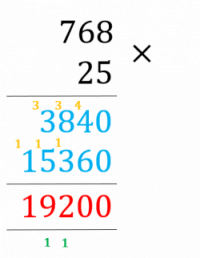
Finally, move the decimal point back the same number of times as before. So, move it 3 times to the left.
The final answer is therefore:
7.68 \times 2.5 = 19.200 = \textcolor{red}{19.2}
Skill 4: Dividing Decimals
To divide decimals without a calculator, use the following steps:
Step 1: Write the division as a fraction.
Step 2: Multiply the top and bottom by 10 until the bottom is no longer a decimal.
Step 3: Complete the bus stop method for dividing numbers without a calculator.
Step 4: This gives the final answer.
Example: Calculate 9.184 \div 1.4
Write the division as a fraction:
9.184 \div 1.4 = \dfrac{9.184}{1.4}
Multiply the top and bottom by 10 until the bottom is no longer a decimal:
\dfrac{9.184 \times 10}{1.4 \times 10} = \dfrac{91.84}{14}
Use the bus stop method to calculate the division:
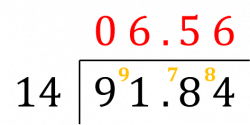
So,
9.184 \div 1.4 = \textcolor{red}{6.56}
Skill 5: Comparing Decimals
You can compare and order decimals, just like you can order numbers. However, ordering decimals is a little harder.
To order decimals, you need to look at each number in turn and compare them starting with the first digit.
Example: Put the following numbers in order from smallest to largest.
1.101, \,\,\, 0.11, \,\,\, 1.10, \,\,\, 0.01
Step 1: Look at the first digit of each number and compare them.
\xcancel{\textcolor{red}{1}.101}, \,\,\, \overset{\downarrow}{\textcolor{red}{0}}.11, \,\,\, \xcancel{\textcolor{red}{1}.10}, \,\,\, \overset{\downarrow}{\textcolor{red}{0}}.01
2 numbers start with 1 and 2 numbers start with 0. Since we want the smallest first, we can eliminate the 2 largest.
Step 2: Now, look at the second digits of each of the remaining numbers and compare them.
\xcancel{0.\textcolor{red}{1}1}, \,\,\, 0.\overset{\downarrow}{\textcolor{red}{0}}1
The second digit for the first number is a 1 and for the second number it is a 0, so the first number it is bigger, so we can eliminate this.
So, the smallest number is 0.01 and 0.11 is the second smallest.
Step 3: Then, look at the other numbers that were previously crossed out, and compare these.
\xcancel{1.{\textcolor{red}{1}} {\textcolor{blue}{0}}{\textcolor{limegreen}{1}}}, \,\,\,\, 1.{\textcolor{red}{1}}{\textcolor{blue}{0}}
Look at the second digit for each number and compare them, but these are the same. So, compare the third digit, but these again are the same.
The first number has a fourth digit, but the second number does not, so eliminate the first number since it is bigger.
So, 1.10 is the third smallest and 1.101 is the biggest.
Step 4: Finally, write down the correct order:
0.01, \,\,\,\, 0.11, \,\,\,\, 1.10, \,\,\,\, 1.101
Functional Skills: Decimals Example Questions
Question 1:
a) In 5.0461, what is the value of the 6?
[1 mark]
b) Which number is bigger, 5.0461 or 5.0470?
[1 mark]
a) The 6 is in the third column after the decimal point, which is the thousandths column. So, it is
\text{six thousandths} or \dfrac{6}{1000}
b) the numbers are the same until the thousandths column. The first number has a 6 in the thousandths column, where as the second number has a 7 in the thousandths column.
Therefore, 5.0470 is bigger than 5.0461
Question 2: Calculate 81.07 + 31.862 without using a calculator.
[2 marks]
Use the column method for addition:
\begin{array}{r}81. 070\\+ 31.862\\\hline 112.932 \\\hline 1\,\,\,\,\,\,\,\,1\,\,\,\,\,\, \end{array}
Question 3: Calculate 18.63 \div 2.3 without using a calculator.
[2 marks]
Turn the division into a fraction,
18.63 \div 2.3 = \dfrac{18.63}{2.3}
Multiply the top and bottom by 10 until the bottom is no longer a decimal:
\dfrac{18.63 \times 10}{2.3\times 10} = \dfrac{186.3}{23}
Now, use the bus stop method,
\begin{array}{c}\;\;\;\;\;\;\;\;\;\;\;\;\;8\;.\;1\\23\overline{\left) \cancel1^1\cancel8^{18}6\;.{}^23\right.}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{array}
So,
18.63\div 2.3 = 8.1
Question 4: Calculate 3.566\times 14 without using a calculator.
[2 marks]
Move the decimal point to the right of the numbers:
Move the decimal point 3 times on 3.566 to make it 3556
14 does not need changing.
So, there have been 3 decimal places moved in total.
Then, use column multiplication (or grid multiplication),
\begin{array}{r}3566\\\times14\\\hline14264\\+35660\\\hline49924 \end{array}
Finally, move the decimal point 3 times to the left, to get the final answer:
3.566 \times 14 = 49.924
Question 5: Calculate 7.473 - 5.261 without using a calculator.
[2 marks]
Use the column method for subtraction:
\begin{array}{r}7.473\\-5.261\\\hline 2.212\end{array}
Specification Points Covered
L1.10 – Read, write, order and compare decimals up to three decimal places
L1.11 – Add, subtract, multiply and divide decimals up to two decimal places
L2.9 – Order, approximate and compare decimals
L2.10 – Add, subtract, multiply and divide decimals up to three decimal places
Functional Skills: Decimals Worksheet and Example Questions
Decimals L1, L2
FS Level 1FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.