Functional Skills: Multiplication
Multiplication
Multiplication means “how many lots of”. The 2 methods used to multiply large numbers without a calculator are the column method and the grid method. If you have a calculator, then multiplication problems are usually straightforward, you just need to know when to multiply.
Make sure you are happy with the following topics before continuing.
When to Multiply
You can recognise questions that require multiplication in two ways:
- Questions that use the word “multiply” or “times“, or similar words like “multiplication“.
- Questions that use the times sign, \times.
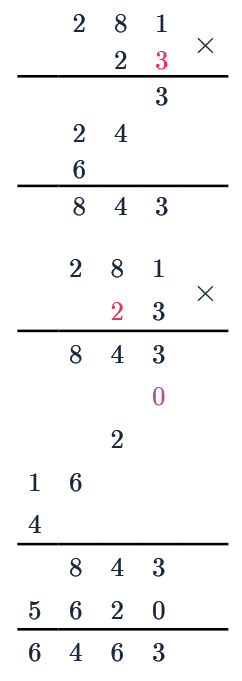
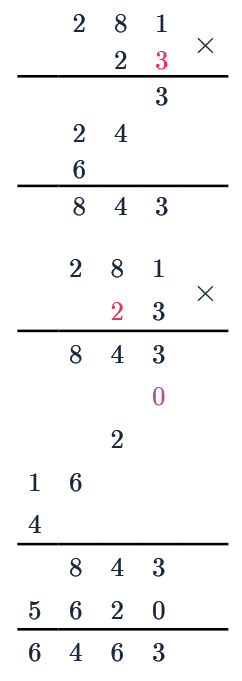
Method 1: Column Method
Example: Calculate 281 \times 23
Step 1: Write the two numbers in the multiplication above each other, with the bigger one on top. Write the values so that the units, the 10s, the 100s etc. all line up in the correct column.
Step 2: Multiply the final digit from the bottom number with every digit from the top number, in turn, and write the results underneath from right to left, making sure to carry forward when the values go above 10.
3\times1 = 3, 3\times8=24, 3\times2 = 6
Step 3: The second digit from the right is the tens digit. For this, write a 0 underneath the previous step’s working so that everything is shifted to the left by one space.
Then, multiply this digit by every digit from the top number, and write the results underneath the last step from right to left.
Step 4: Add up the final numbers using column method for addition, and write the results under another line.
Therefore,
281 \times 23 = \textcolor{black}{6463}
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Method 2: Grid Method
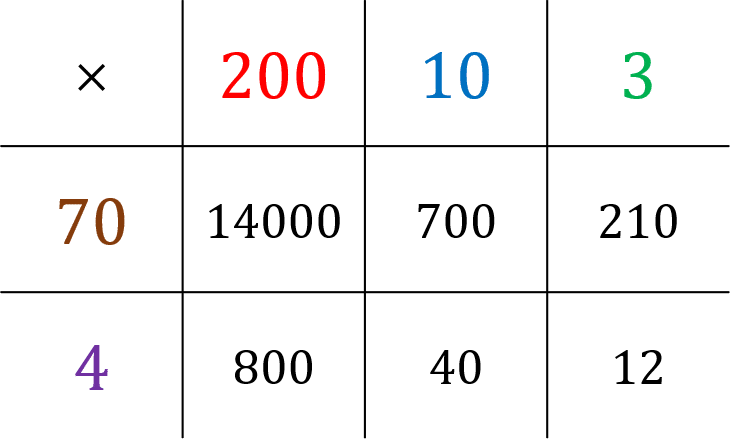

Example: Calculate 213 \times 74
Step 1: Split each number into units, 10s, 100s etc. and write each part of one number along the left side of the grid, and each part of the other number across the top.
\textcolor{red}{2} = \textcolor{red}{200}
\textcolor{blue}{1} = \textcolor{blue}{10}
\textcolor{limegreen}{3} = \textcolor{limegreen}{3}
\textcolor{maroon}{7} = \textcolor{maroon}{70}
\textcolor{purple}{4} = \textcolor{purple}{4}
Step 2: Fill in each square of the grid by individually multiplying each part of one number by each part of the other number.
Step 3: Finally, add up all answers from the grid to get the final answer:
14000+700+210+800+40+12= \textcolor{black}{15762}
Multiplying on a Calculator
The above methods are for multiplying without a calculator. Multiplying with a calculator is much simpler. You press each digit individually for the first number, then the times symbol which looks like this: \times, then each digit individually for the second number, then equals.
Example: Multiply 23 and 571 using a calculator.
Press 2 then 3 then \times then 5 then 7 then 1 then =

You should see a result of 13133.
Multiplying by \boldsymbol{10}, \boldsymbol{100} and \boldsymbol{1000}
- To multiply by \textcolor{red}{\boldsymbol{10}}, you move the decimal point one place to the right.
- To multiply by \textcolor{red}{\boldsymbol{100}}, you move the decimal point two places to the right.
- To multiply by \textcolor{red}{\boldsymbol{1000}}, you move the decimal point three places to the right.
This rule can be used for multiplying by 10000, 100000..., just move the decimal point to the right the same amount as the amount of zeros after the 1.
Remember: For whole numbers the decimal point doesn’t look like it’s there, but it is. For example 25 can be written as 25.0
Square Numbers
Multiplying a number by itself is called squaring a number, for instance 6 squared =6\times6=36
Often squared numbers are written using a small 2 – e.g. 6^2
For more difficult squares, like 19^2, if you don’t have a calculator you may have to use the multiplication methods described above, or break the multiplication down into smaller chunks.
Example 1: Multiplication Problems
Aimee buys \textcolor{blue}{60} boxes of pencils for her school. Each box contains \textcolor{red}{40} pencils, with each pencil costing 15p.
How much does she spend on pencils altogether?
[2 marks]
We need to calculate the cost for one box of pencils:
Cost of 1 box = \textcolor{red}{40} \times 15 = 600p
Then multiply by the number of boxes, 60, to find the total cost:
Total cost = 600 \times \textcolor{blue}{60} = 36000p =\textcolor{blue}{£360}
Example 2: Multiplying by \boldsymbol{10}, \boldsymbol{100} and \boldsymbol{1000}


Calculate:
a) 5.7\times100
b) 42\times10
c) 13.1\times1000
[3 marks]
Example 3: Square Numbers
Calculate:
a) 13^2
b) 22^2
[2 marks]
a) 13^2=13\times13=10\times13+3\times13=130+39=169
b) 22^2=22\times20+22\times2=440+44=484
Functional Skills: Multiplication Example Questions
Question 1: Calculate 45 \times 619, without the use of a calculator.
[3 marks]
Here, we will use the long multiplication method, multiplying 619 by 5 and then by 40, and then adding the results:
\begin{array}{r}619\\\times45\\\hline3095\\+24760 \\\hline27855 \end{array}
Question 2: Calculate 52 \times 31, without the use of a calculator.
[3 marks]
Here, we will use the long multiplication method, multiplying 52 by 1 and then by 30, and then adding the results:
\begin{array}{r}\begin{array}{r}52\\\times31\\\hline52\\+1560\\\hline 1612\end{array}\end{array}
Question 3: Mark buys 15 packs of paving slabs for his drive. Each pack contains 8 paving slabs. The cost of each paving slab is £9.
How much does mark spend on paving slabs in total?
[2 marks]
We need to calculate the cost for one pack of paving slabs:
Cost of 1 pack = 8 \times £9 = £72
Then multiply by the number of packs, 15, to find the total cost:
Total cost = 15 \times £72 = £1080
Question 4: Calculate the following:
a) 5.61\times100
b) 13\times10000
c) 0.73\times10
[3 marks]
a) Multiplying by 100 means we move the decimal point two places to the right.
So
5.61\times100=561
b) Multiplying by 10000 means we move the decimal point four places to the right.
So
13\times10000=130000
c) Multiplying by 10 means we move the decimal point one place to the right.
So
0.73\times10=7.3
Question 5: Calculate the following:
a) 8^2
b) 11^2
c) 26^2
[3 marks]
a) 8^2=8\times8=64
b) 11^2=11\times11=121
c) 26^2=26\times26=26\times20+26\times6=520+156=676
Specification Points Covered
EL3.4 – Multiply two-digit whole numbers by single and double digit whole numbers
L1.3 – Multiply and divide whole numbers and decimals by 10, 100, 1000
L1.4 – Use multiplication facts and make connections with division facts
L1.6 – Calculate the squares of one-digit and two-digit numbers
L2.2 – Carry out calculations with numbers up to one million including strategies to check answers including estimation and approximation
Functional Skills: Multiplication Worksheet and Example Questions
Multiplication E3
Entry Level 3NewOfficial PFSMultiplication L1
FS Level 1NewOfficial PFSMultiplication L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.