Functional Skills: Surface Area
Functional Skills: Surface Area Revision
Calculating the Surface Area
You may be given the area of each face of a 3D shape, or you will more likely be given the dimensions and have to work out the area of each face individually.
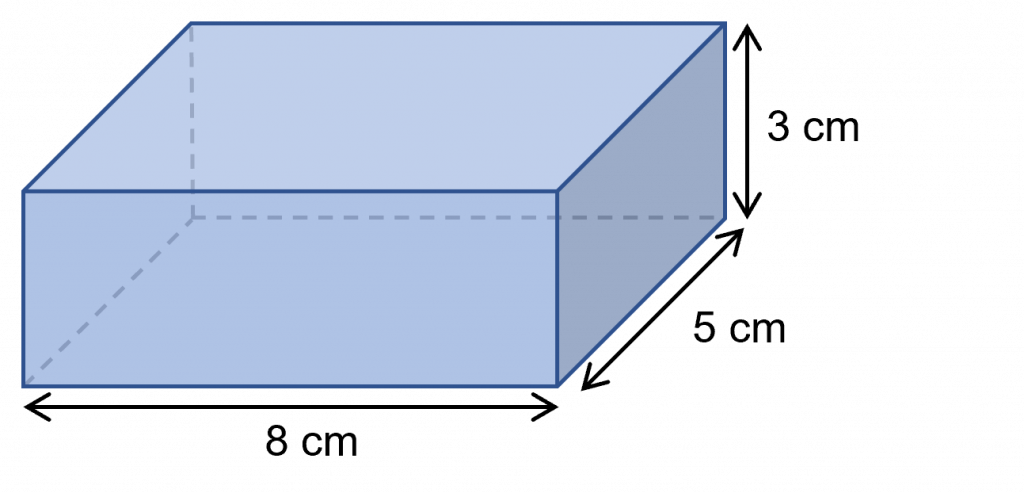

Example: Calculate the surface area of the cuboid.
The area of the front face and back face are both \textcolor{blue}{8} \times \textcolor{blue}{3} = 24 \text{ cm}^2
The area of the side faces are both \textcolor{blue}{5} \times \textcolor{blue}{3} = 15\text{ cm}^2
The area of the top face and bottom face are both \textcolor{blue}{8} \times \textcolor{blue}{5} = 40\text{ cm}^2
Therefore, the total surface area is
(2 \times 24) + (2 \times 15) + (2 \times 40) = 48 + 30 + 80 = 158 \text{ cm}^2
Using Nets to find the Surface Area
You can use nets to help find the surface area. This will help when calculating the surface area of all 3D shapes, especially prisms and cylinders.
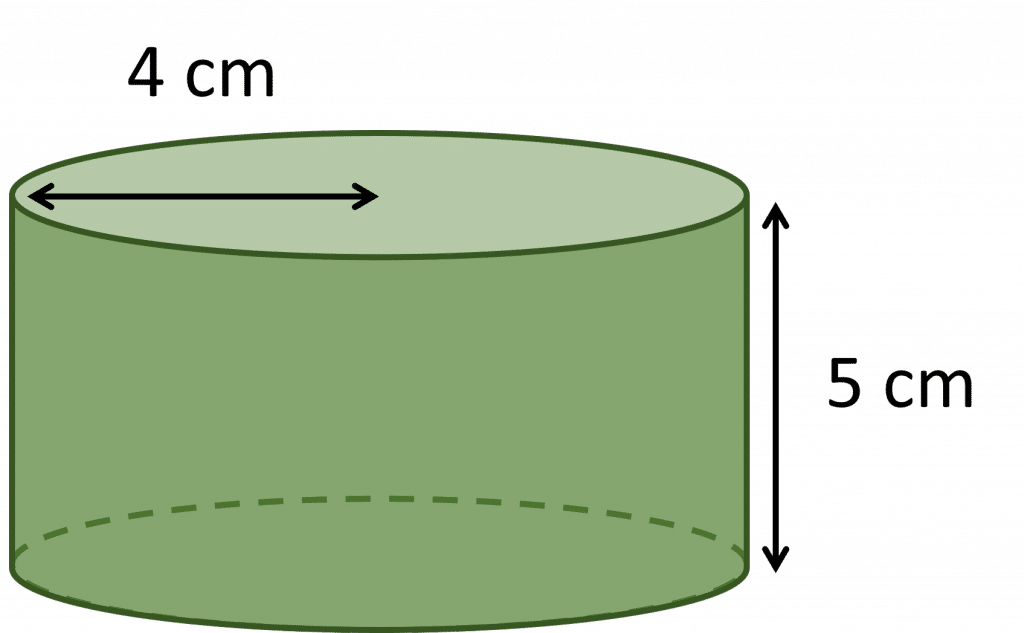

Example: Calculate the surface area of the cylinder.
Give your answer to the nearest whole number.
Use \pi = 3.14
You can draw the net of this cylinder to help:
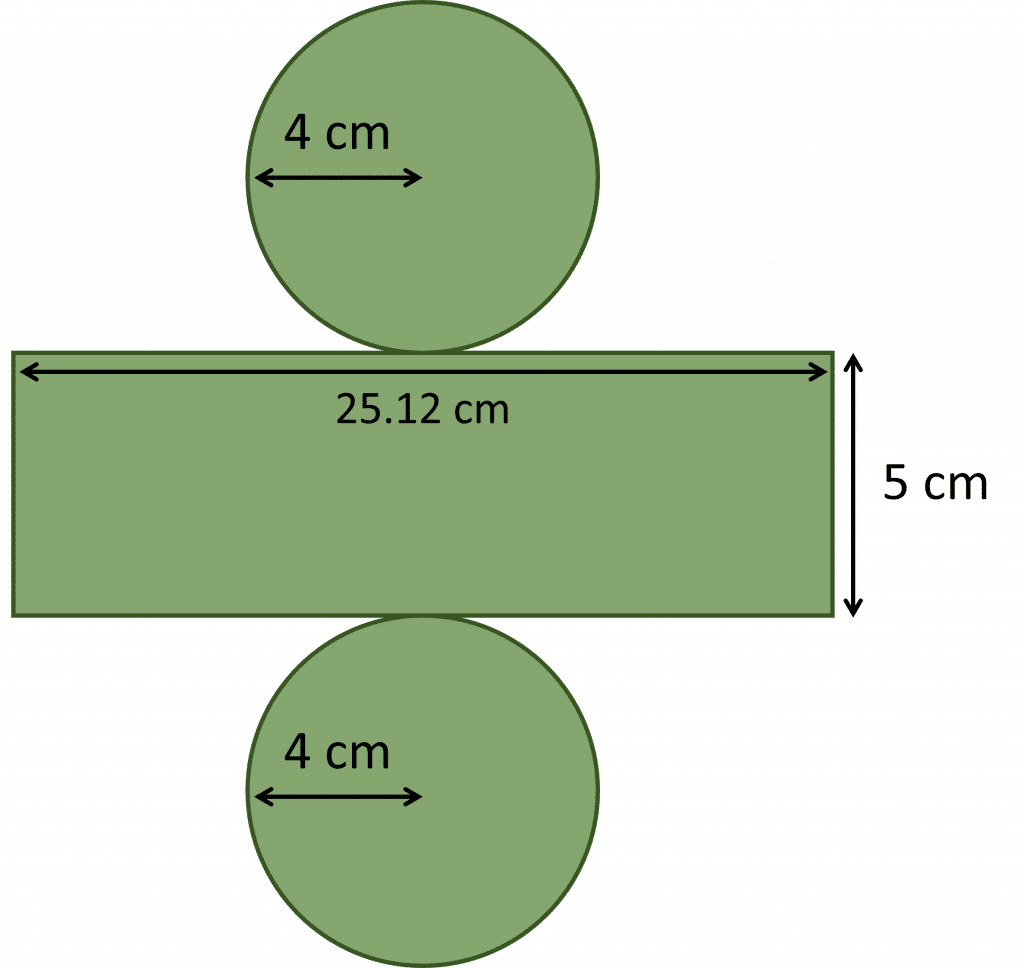

The net has two circles of radius \textcolor{red}{4} cm, and a rectangle of width \textcolor{blue}{5} cm and length which is equal to the circumference of the circles.
First, calculate the circumference of the circle:
circumference = \pi d = 2 \pi r = 2 \times 3.14 \times \textcolor{red}{4} = 25.12 cm
Then, calculate the areas of the faces:
area of rectangle = 25.12 \times \textcolor{blue}{5} = 125.6 cm^2
area of circle =\pi r^2 = 3.14 \times \textcolor{red}{4}^2 = 50.24 cm^2
So, add the areas of all the faces together, to find the surface area of the cylinder:
surface area of cylinder = 50.24 + 50.24 + 125.6 = 226.08 = 226 cm^2
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Example: Surface Area of a Pyramid
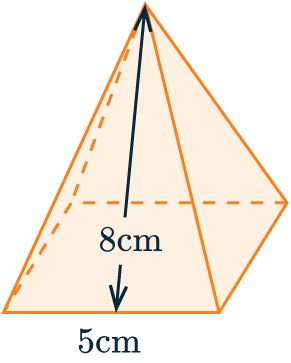

Calculate the surface area of the pyramid.
[4 marks]
All 4 triangular faces are equal.
So, we can calculate the area of one triangle and multiply it by 4 to get the area of all of them.
Area of triangle = \dfrac{1}{2} \times b \times h = \dfrac{1}{2}\times5\times8=20 cm^2
Therefore, the area of all 4 triangles is
4\times20=80 cm^2
Now, we need to find the area of the square base,
Area of base =5 \times 5=25 cm^2
Therefore, the surface area is the area of each face added together:
Total surface area =25+80=105 cm^2
Functional Skills: Surface Area Example Questions
Question 1: A cube has sides of length 7 cm.
Calculate the surface area of the cube.
[2 marks]
The area of one square face is
7 \times 7 = 49 cm^2
Therefore, since a cube has 6 square faces, the surface area is
6 \times 49 = 294 cm^2
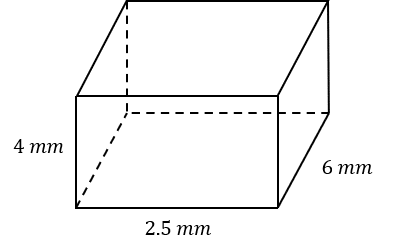
Question 2: Below is a cuboid with length 6 mm, width 2.5 mm, and height 4 mm.
Calculate the surface area of the cuboid.
[3 marks]
Area of front face:
4\times2.5=10 mm^2
Therefore, the back face also has area 10 mm^2
Area of right side face:
6\times4=24 mm^2
Therefore, the left side face also has area 24 mm^2
Area of top face:
6\times2.5=15 mm^2
Therefore, the bottom face also has area 15 mm^2
Total surface area:
10+10+24+24+15+15=98 mm^2
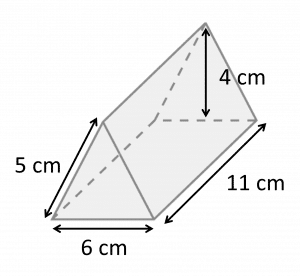
Question 3: Calculate the surface area of the prism in the diagram below.
[4 marks]
The area of the front triangular face is
\dfrac{1}{2} \times 6 \times 4 = 12 cm^2
The area of the back triangular face is therefore 12 cm^2 also.
The area of a slanted rectangular face is
11 \times 5 = 55 cm^2
The area of the other slanted rectangular face is also 55 cm^2
The area of the rectangular base is
11 \times 6 = 66 cm^2
Therefore, the total surface area is
12 + 12 + 55 + 55 + 66 = 200 cm^2
Functional Skills: Surface Area Worksheet and Example Questions
Surface Area L2
FS Level 2NewOfficial PFS[responsive-flipbook id=”pfs_pocket_revision_guide_-_sample”]
Revision Products

Functional Skills Maths Level 2 Pocket Revision Guide
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact revision guide.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.