Functional Skills: Area
Area
The area of 2D shape is the amount of surface it occupies.
Area is calculated by multiplying lengths together, so the metric units for area are squared – cm^2, m^2, mm^2 etc. For imperial units for area, we usually say square inches (sq. in) instead of in^2, for example.
You will need to know 4 skills to calculate the area of a square, a rectangle, a triangle and compound shapes.


Skill 1: Area of a Square
The formula for the area of a square is:
\text{Area} =a \times a = a^2
where a is the length of the sides of the square.
Written in words, this is:
\text{Area} = \text{length} \times \text{length} = \text{length}^2
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.


Skill 2: Area of a Rectangle
The formula for the area of a rectangle is:
\text{Area} = a\times b
where a is the width of the rectangle and b is the length.
Written in words, this is:
\text{Area} = \text{width} \times \text{length}
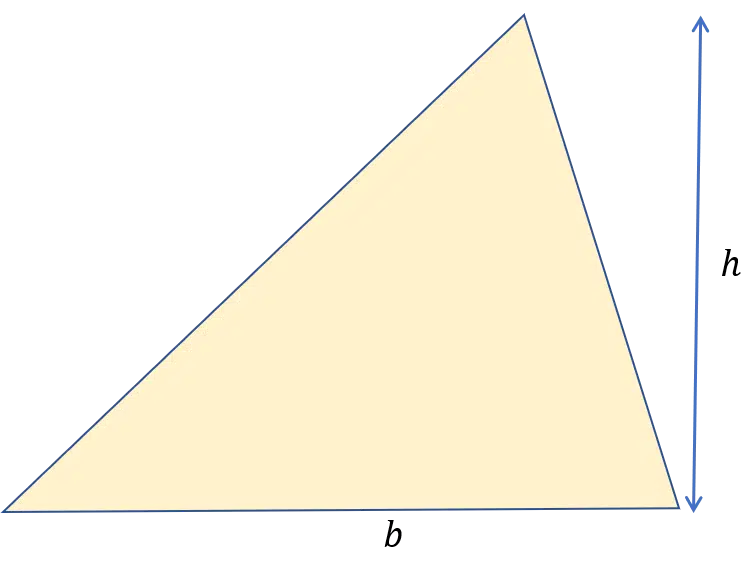

Skill 3: Area of a Triangle
The formula for the area of a triangle is:
\text{Area} = \dfrac{1}{2}\times b \times h
where b is the base width of the triangle and h is the vertical height as shown in the diagram on the right.
Written in words, this is:
\text{Area} = \dfrac{1}{2} \times \text{base} \times \text{height}
Skill 4: Area of Compound Shapes
Sometimes, you may need to split up a compound shape into easier shapes to find the area.


Example: Find the area of the shape to the right.
For this shape you could either:
- Split the shape up into two rectangles, calculate the area of each rectangle and add them up.
- Notice that the shape is a large rectangle, with a smaller rectangle cut out of it. So, we could calculate the area of the smaller rectangle and minus it from the larger rectangle. This would be easier in this situation:
\text{Area of larger rectangle} = 7 \times 12.5 = \textcolor{red}{87.5 \text{ m}^2}
\text{Area of smaller rectangle} = 5 \times 10 = \textcolor{blue}{50 \text{ m}^2}
\text{Area of shape} = \textcolor{red}{87.5} - \textcolor{blue}{50} = \textcolor{limegreen}{37.5 \text{ m}^2}
Example 1: Area of a Square
Calculate the area of a square with sides of length 6 \text{ cm}.
[1 mark]
\text{Area of square} = 6 \times 6 = 6^2 = 36 \text{ cm}^2
Example 2: Area of a Rectangle


Calculate the area of the rectangle shown to the right.
[2 marks]
\text{Area of rectangle} = 12 \times 5 = 60 \text{ cm}^2
Example 3: Area of a Triangle
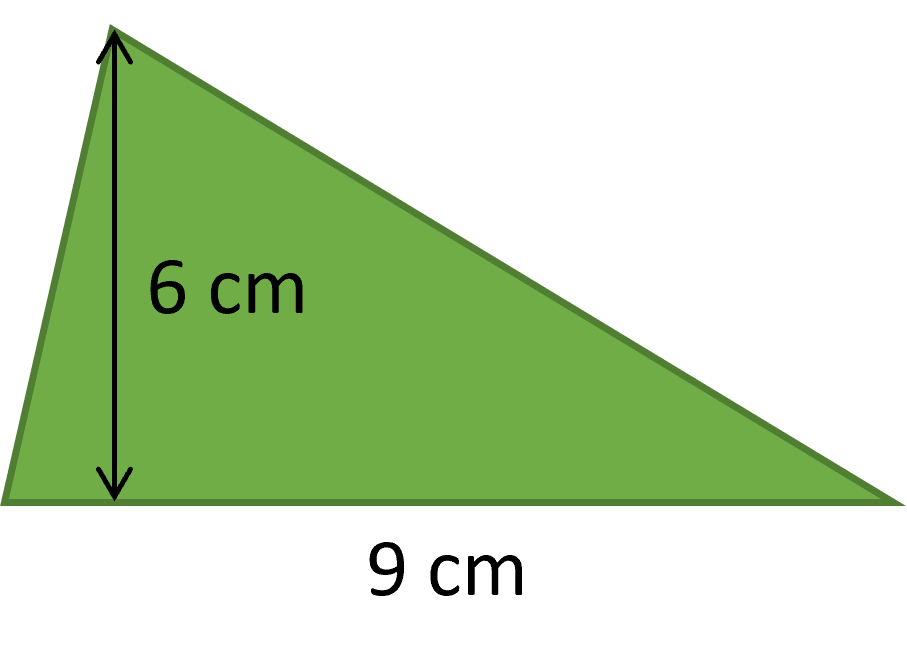

Calculate the area of the triangle shown to the right.
[2 marks]
\text{Area of triangle} = \dfrac{1}{2} \times 9 \times 6 = 27 \text{ cm}^2
Functional Skills: Area Example Questions
Question 1: Calculate the area of the triangle ABC shown below, which has a base of 9.8 cm and a height of 11.2 cm.
[2 marks]
Using the formula for the area of a triangle:
Area = \dfrac{1}{2}\times base \times height
Area = \dfrac{1}{2}\times 9.8 \times 11.2=54.88 cm^2
Question 2: Calculate the area of the rectangle shown below.
[1 mark]
Area of a rectangle = width \times length
Area = 5.1\times7.6=38.76 cm^2
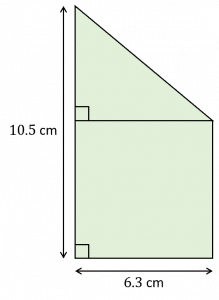
Question 3: Below is a right-angled triangle on top of a square. Using the measurements given, calculate the area of the whole shape.
[3 marks]
Area of the Square = 6.3\times 6.3=39.69 cm^2
To work out the area of the triangle we need to know the height. This can be found by subtracting the side length of the square from the total height of the shape: 10.5-6.3=4.2 cm
Area of the triangle = \dfrac{1}{2}\times6.3\times4.2=13.23 cm^2
Total area = 39.69 + 13.23 = 52.92 cm^2
Specification Points Covered
L1.22 – Calculate the area and perimeter of simple shapes including those that are made up of a combination of rectangles
L2.16 – Calculate perimeters and areas of 2-D shapes including triangles and circles and composite shapes including non-rectangular shapes (formulae given except for triangles and circles)
Functional Skills: Area Worksheet and Example Questions
Area L1
FS Level 1NewOfficial PFSArea L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.