Functional Skills: Numbers and Place Value
Functional Skills: Numbers and Place Value Revision
Numbers and Place Value
Numbers can be split up into columns, called digits. Place value is about the value of each digit within a number. Each digit has a different value determined by its position in the number.
Place Value
The value of each digit decreases, going from left to right. Each digit in the number has a different value, e.g. the 5 means 50,000. The value for each digit added together makes the number.
To read or write a large number, break up the number into groups of three digits starting from the right, using commas if we wish.
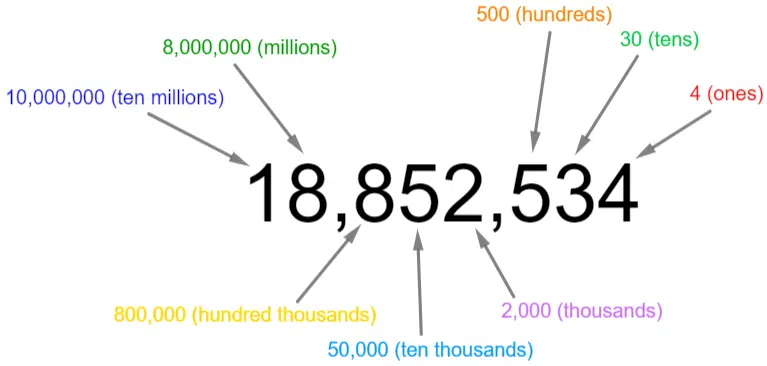
We then have a millions group, a thousands group and the rest. Therefore, this number can be spoken in words as
18 million, 852 thousand, 5 hundred and 34
or
eighteen million, eight hundred and fifty-two thousand, five hundred and thirty-four
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Positive and Negative Numbers
Numbers can either be positive, if they are greater than 0, or negative, if they are less than 0.
Number lines can help you visualise certain number problems, for instance they are really helpful in allowing you to grasp the concept of negative numbers. They can also be useful to find the difference between two numbers.
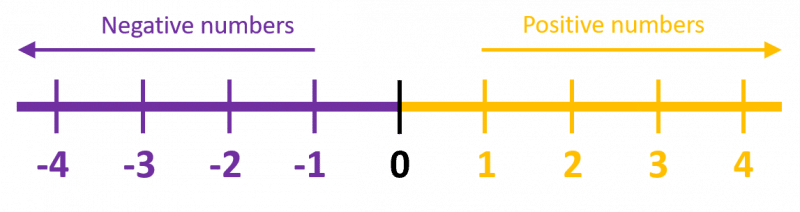
The further right you go on the number line, the larger the numbers become, e.g. 3 is larger than -1 which is larger than -2
Scales
Scales are just number lines that are often used in real life scenarios, for example a thermometer.
Sometimes they don’t always show every number and just increase in intervals.
The ruler below is an example of a scale, used to measure lengths.
Example 1: Place Value
State the place value of the 6 in 5609.
[1 mark]
Counting from right to left, we can see that the 6 is in the third column along – the hundreds column.
Therefore, the value of the ‘6 digit’ in this number is 600.
Example 2: Positive and Negative Numbers
Which number is larger, -3 or -8?
[1 mark]
Because both of these numbers are negative, so the number which is larger is the one with a smaller number after the minus (-) sign, which is -3
Example 3: Number Line
The temperature at night was -3 \degreeC, and then the temperature in the daytime was 11\degreeC.
Work out the difference between the temperature at night and in the daytime.
[1 mark]
First draw a number line that includes both -3 and 11.
Then count on from -3 to 11.
As shown on the number line above, there area 14 steps, so the difference is \boldsymbol{14\degree}C.
Example 4: Scales
Elise is measuring the height of a box, using a centimetre ruler.
What is the height of the box?
[1 mark]
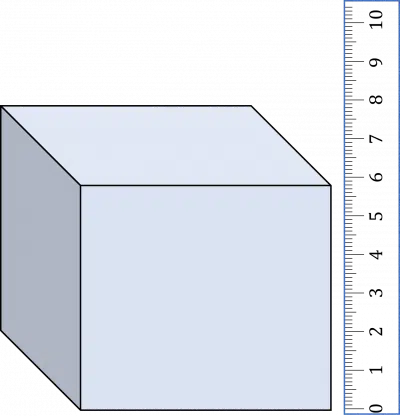
Each small line between whole numbers is worth 0.1 cm, and the height of the box is 8 lines between 5 and 6, so the height of the box is 5.8 cm.
Functional Skills: Numbers and Place Value Example Questions
Question 1: What is the value of the 8 in 1899?
[1 mark]
The 8 is the 3rd digit from the right, meaning it’s in the hundreds column. So, the value is,
800 or \text{eight hundred}
Question 2: What is the value of the 5 in 527023?
[1 mark]
The 5 is the 6th digit from the right, meaning it’s in the hundred thousands column. So, the value is,
500000 or \text{five hundred thousand}
Question 3: How is the number 475210 spoken in words?
[1 mark]
Split the number into groups of three, starting from the right. So we have a thousands group and the rest.
475210 is therefore spoken as
475 \text{ thousand } 2 \text{ hundred and } 10
or
\text{four hundred and seventy-five thousand, two hundred and ten}
Question 4: How is the number fifty-three thousand, one hundred and four written in numbers?
[1 mark]
\text{fifty-three thousand} = 53000
\text{one hundred} = 100
\text{four} = 4
These can then be added together to make the number:
53104
Question 5: Which number is smaller, -23 or -24?
[1 mark]
Because both of these numbers are negative, so the number which is smaller is the one with a larger number after the minus (-) sign, which is -24
Question 6:Â Use a number line to find the difference between -4 and 5.
[1 mark]
As shown by the number line above, there are 9 steps between -4 and 5, so the difference is 9.
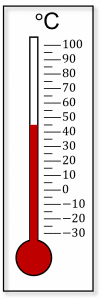
Question 7:Â The thermometer below shows the temperature of some water in \degreeC.
What temperature is the water?
[1 mark]
We can see that the temperature is halfway between 40\degreeC and 50\degreeC. So the temperature of the water is 45\degreeC.
Functional Skills: Numbers and Place Value Worksheet and Example Questions
Numbers and Place Value L1
FS Level 1NewOfficial PFS
Numbers and Place Value L2
FS Level 2NewOfficial PFS[responsive-flipbook id=”pfs_pocket_revision_guide_-_sample”]
Revision Products
Functional Skills Maths Level 2 Pocket Revision Guide
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact revision guide.
Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.
Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.
Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.
Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.
