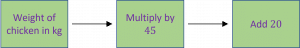Functional Skills: Formulas
Formulas
A formula is a rule used to calculate a value. They can be written 2 different ways, either using words or letters. You may also see formulas expressed as function machines.
Make sure you are happy with the following topics before continuing.
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Type 1: Formulas Using Words
You will need to interpret a question and produce a formula from it. They may have one, or more than one step in them.
Example: Radamel wants to hire a car for \textcolor{red}{12} days. The car hire company charges a £75 fixed fee for hiring the car, plus £12.50 per day of hiring. How much would it cost for Radamel to hire the car for \textcolor{red}{12} days?
This formula means £12.50 per day plus £75. This can be written as an formula with 2 steps:
Step 1: £12.50 \times \text{number of days}
Step 2: + \, £75
So, put this into a single formula:
\text{Cost of car hire} = (£12.50 \times \text{number of days}) + £75
Then, you need to put the missing numbers in. Here, ‘number of days’ =\textcolor{red}{12}
\text{Cost of car hire} = (£12.50 \times \textcolor{red}{12}) + £75 = \textcolor{limegreen}{£225}
Type 2: Formulas Using Letters
You may also need to convert words into letters, or be able to use formulas given in terms of letters.
For formulas using letters, you need to replace each letter with a number. Some formulas don’t use \times and \div, for example, instead, a \times b may be written as ab and a \div b may be written as \dfrac{a}{b}.
Example: A spherical football has a radius of \textcolor{blue}{11} cm. The surface area of a sphere is given by the formula
A = 4\pi r^2
where A is the surface area, r is the radius and take \pi = 3.14
What is the surface area of the football? Give your answer in cm^2 to the nearest 10.
The radius of the football is \textcolor{blue}{11} cm, so \textcolor{blue}{\textit{r} = 11}
Substitute the value of each letter into the formula, to find the surface area of the football:
\begin{aligned} A &= 4\pi r^2 \\ &=4 \times 3.14 \times \textcolor{blue}{11}^2 \\ &= 4 \times 3.14 \times 121 \\ &= 1519.76 = \textcolor{limegreen}{1520 \text{ cm}^2} \text{ (to the nearest 10)} \end{aligned}
Type 3: Function Machines
Function machines can help you break down a formula that has more than one step in it. They are useful, as they allow you to visualise the order of steps.
Example: This function machine helps you to work out how much Tony is going to be charged by the plumber he has hired.

The plumber worked for \textcolor{purple}{48} hours in total.
Work out how much Tony will be charged.
Step 1: Put in \textcolor{purple}{48} into the function machine – in place of ‘Hours worked’.
Step 2: Then follow the rest of the steps.

Functional Skills: Formulas Example Questions
Question 1: Mandy works in a shoe factory. She can make 15 pairs of shoes in a day. How many pairs of shoes can she make in 6 days?
[1 mark]
The formula is:
Number of pairs of shoes = 15 \times number of days
We want to find the number of pairs of shoes she can make in 6 days, so we put 6 into the formula:
Number of pairs of shoes = 15 \times 6 = 90
Question 2: Michelle pays for a gardener to cut her grass. The gardener charges a fixed fee of £15 plus £0.50 per \text{ m}^2 of grass. Michelle’s grass is 45\text{ m}^2 in area.
How much does Michelle pay for the gardener to cut her grass?
[2 marks]
This formula means £15 plus £0.50 per \text{ m}^2. This can be written as a formula with 2 steps:
\text{Cost of gardener} = (£0.50 \times \text{area of grass in m}^2) + £15
Then, put in the missing numbers. Here, the area of grass is 45\text{ m}^2:
\text{Cost of gardener} = (£0.50 \times 45) + £15 = £37.50
Question 3: Calculate the value of \dfrac{3a^2}{5b} when a = 4 and b = 3
[1 mark]
Substitute a = 4 and b = 3 into the equation:
\dfrac{3 \times 4^2}{5 \times 3} = \dfrac{48}{15} = 3.2
Question 4: Manique needs to pay for a taxi. The cost of the taxi is calculated using the formula below:
\text{cost} = 0.5(3 + 5m)
Where m is the number of miles driven.
Manique travels 6.2 miles and pays with a £20 note. How much change would she receive from a £20 note?
[2 marks]
Put the value of m=6.2 into the formula:
\text{cost} = 0.5(3 + 5 \times 6.2) = £17
So, from a £20 note she would receive
£20 - £17 = £3
Question 5: The following formula describes the volume of a gas under specific conditions:
V = \dfrac{nRT}{P}
where V is the volume of the gas in m^3
n is the number of moles (a fixed amount) of a gas
R = 8.31 is the ideal gas constant
T is the temperature of the gas in Kelvin (K)
P is the pressure of the gas in Pascals (Pa)
Calculate the volume of 3 moles of gas at a temperature of 300 K, when the pressure is 100000 Pa.
Give your answer to 3 decimal places.
[2 marks]
We first need to work out what the value of each number is:
n = 3
R = 8.31
T = 300
P = 100000
Then, substitute them into the formula, to find the volume of the gas:
V = \dfrac{3 \times 8.31 \times 300}{100000} = \dfrac{7479}{100000} = 0.07479 = 0.075 (3 dp)
Question 6: Anne is going to cook a 2.5 kg chicken for a roast dinner. Use the function machine below to work out how long Anne will need to cook her chicken for (in minutes).
[2 marks]
Substituting in 2.5 kg into the function machine:
2.5\times45 +20=112.5+20=132.5 minutes
Specification Points Covered
L1.5 – Use simple formulae expressed in words for one or two-step operations
L2.3 – Evaluate expressions and make substitutions in given formulae in words and symbols
Functional Skills: Formulas Worksheet and Example Questions
Formulas L1
FS Level 1NewOfficial PFSFormulas L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.