Functional Skills: Fractions, Decimals and Percentages
Functional Skills: Fractions, Decimals and Percentages Revision
Fractions, Decimals and Percentages
Here we will look at how to convert between fractions, decimals, and percentages. All 3 forms are equivalent ways of saying the same thing, but we normally use the one that is most appropriate in that particular scenario.
For LEVEL 1, you will only need convert between fractions, decimals, and percentages, that when converted to a percentage are a multiple of 5\%, e.g. 5\%, 10\%, 50\% etc. For LEVEL 2 you will need to use these skills for more complicated percentages, e.g. 2\%, 12.5\% etc.
Make sure you are happy with the following topics before continuing.
Question - How do I improve my chances of passing the level 2 maths exam?
Answer – Pre-assessment. This useful tool identifies the key areas of the exam you will need to work on in order to pass your level 2 exam for the first time.
Common Conversions
Fractions, decimals and percentages conversions are really useful to memorise.
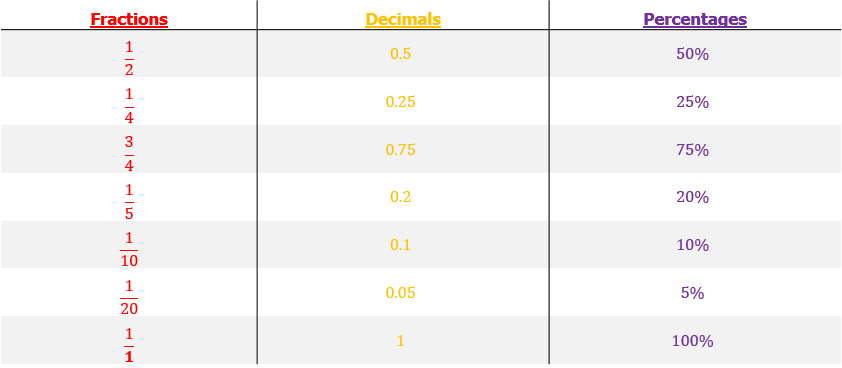
These are some common fractions, decimals and percentages you should remember.
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Converting Fractions to Decimals to Percentages
Fractions to Decimals:
Treat the fraction like a division, so divide the top number of the fraction by the bottom number,
e.g. \dfrac{13}{20} = 13 \div 20 = 0.65
Decimals to Percentages:
Multiply the decimal by 100 (i.e. move the decimal point 2 places to the right) and add a \% sign,
e.g. 0.65 \times 100 = 65\%
Note: Convert fractions to percentages by converting the fraction to a decimal and then the decimal to a percentage
e.g. \dfrac{65}{100} = 0.65 = 65\%
Converting Percentages to Decimals to Fractions
Percentages to Decimals:
Divide by 100 (i.e. move the decimal point 2 places to the left) and remove the \% sign,
e.g. 65\% \div 100 = 0.65
Decimals to Fractions:
Write the decimal as a fraction with 1 on the bottom. Then, repeatedly multiply the top and the bottom of the fraction by 10 until the top number turns into a whole number,
e.g. 0.65 = \dfrac{0.65}{1} = \dfrac{6.5}{10} = \dfrac{65}{100}
Then, you can simplify the fraction if needed: \dfrac{65}{100} = \dfrac{13}{20}
Note: To convert straight from percentages to fractions, write the percentage as a fraction with 100 on the bottom, without the \% sign, and then simplify it
e.g. 65\% = \dfrac{65}{100} = \dfrac{13}{20}
Comparing Fractions, Decimals and Percentages – Level 1
For Level 1, you will only need to be able to compare and order fractions, decimals and percentages, that when converted to a percentage are a multiple of 5.
Example: Put the following in order from smallest to largest:
25\%Â Â Â Â Â \dfrac{1}{5}Â Â Â Â Â \dfrac{3}{20}Â Â Â Â Â 0.3
Step 1: Convert all of the numbers into the same form (converting all to decimals is usually the easiest):
25\% = 0.25
\dfrac{1}{5} = 0.2
\dfrac{3}{20} = 0.15
Step 2: Rewrite the list as decimals:
0.25Â Â Â Â Â 0.2Â Â Â Â Â 0.15Â Â Â Â Â 0.3
Step 3: Put the list in order from smallest to largest, using the technique of ordering decimals:
0.15Â Â Â Â Â 0.2Â Â Â Â Â 0.25Â Â Â Â Â 0.3
Step 4: Write down the order, converting the decimals back into their original form:
\dfrac{3}{20}Â Â Â Â Â \dfrac{1}{5}Â Â Â Â Â 25\%Â Â Â Â Â 0.3
Comparing Fractions, Decimals and Percentages – Level 2
You will need to be able to compare and order fractions, decimals and percentages.
Example: Put the following in order from smallest to largest:
23\%Â Â Â Â Â \dfrac{1}{4}Â Â Â Â Â \dfrac{6}{25}Â Â Â Â Â 0.245
Step 1: Convert all of the numbers into the same form (converting all to decimals is usually the easiest):
23\% = 0.23
\dfrac{1}{4} = 0.25
\dfrac{6}{25} = 0.24
Step 2: Rewrite the list as decimals:
0.23Â Â Â Â Â 0.25Â Â Â Â Â 0.24Â Â Â Â Â 0.245
Step 3: Put the list in order from smallest to largest, using the technique of ordering decimals:
0.23Â Â Â Â Â 0.24Â Â Â Â Â 0.245Â Â Â Â Â 0.25
Step 4: Write down the order, converting the decimals back into their original form:
23\%Â Â Â Â Â \dfrac{6}{25}Â Â Â Â Â 0.245Â Â Â Â Â \dfrac{1}{4}
Example 1: Converting Percentages and Decimals
a) Write 47\% as a decimal.
[1 mark]
Divide by 100 and remove the \%, so,
47 \div 100 = 0.47
b) Write 0.548 as a percentage.
[1 mark]
Multiply by 100 and add a \% sign, so,
0.548 \times 100 = 54.8\%
Improve your chances of passing your functional skills maths exam.
Take a pre-assessment and understand what topic areas you need to work on to ensure you pass for level 2 maths exam first time.
Example 2: Converting Fractions and Decimals
a) Write \dfrac{11}{20} as a decimal.
[2 marks]
For a quick method, notice that 20\times 5=100 and dividing by 100 is easy. So, multiply the top and bottom of the fraction by 5 to get
\dfrac{11\times 5}{20\times 5} =\dfrac{55}{100}=0.55
b) Write \dfrac{11}{8} as a decimal.
[2 marks]
Here, we just need to divide 11 by 8. The best way to do this is to use the bus stop method:
So,
\dfrac{11}{8} = 1.375
c) Write 3.76 as a fraction in its simplest form.
[2 marks]
Write the decimal as a fraction with a 1 on the bottom. Then, repeatedly multiply the top and the bottom of the fraction by 10 until the top number turns into a whole number,
\dfrac{3.76}{1}=\dfrac{37.6}{10} = \dfrac{376}{100}
Finally, simplify the fraction:
\dfrac{376}{100} = \dfrac{188}{50} = \dfrac{94}{25}
Example 3: Converting Percentages and Fractions
a) Write 28.5\% as a fraction in its simplest form.
[2 marks]
Percentages are out of 100, so write it as a fraction with 100 on the bottom:
28.5\%=\dfrac{28.5}{100}
Then, multiply the top and bottom by 10 (to make them whole numbers):
28.5\% = \dfrac{285}{1000}
Finally, simplify the fraction:
\dfrac{285}{1000} = \dfrac{57}{200}
b) Write \dfrac{3}{5} as a percentage.
[2 marks]
Firstly, convert the fraction to a decimal. Notice that,
\dfrac{3}{5}=\dfrac{3\times 2}{5\times 2} = \dfrac{6}{10}
So,
6\div 10 = 0.6
Then, to convert this decimal to a percentage, by multiplying by 100 and adding a \% sign:
0.6 \times 100 = 60\%
Example 4: Converting Fractions, Decimals and Percentages
a) Write 85\% as a decimal.
[1 mark]
Divide by 100 and remove the \%, so,
85\div 100=0.85
b)Â Write 0.35 as a percentage.
[1 mark]
Multiply by 100 and add a \% sign, so,
0.35\times 100=35\%
c)Â Write \dfrac{9}{20} as a decimal.
[1 mark]
For this fraction, to work out what it is equivalent as a decimal, we can convert the fraction so the denominator is 100.
\dfrac{9}{20}=\dfrac{45}{100}=0.45
d) Write \dfrac{3}{4} as a percentage.
[2 marks]
Firstly, convert the fraction to a decimal then to a percentage.
\dfrac{3}{4}=0.75=75\%
Functional Skills: Fractions, Decimals and Percentages Example Questions
Question 1: Write 19.4\% as a decimal.
[1 mark]
Divide by 100 and remove the \% sign:
19.4\%\div100=0.194
Question 2: Write 12.5\% as a fraction in its simplest form.
[2 marks]
Write the percentage as a fraction with 100 on the bottom:
12.5\% = \dfrac{12.5}{100}
Now, multiply the top and bottom by 10 so that both numbers are whole:
\dfrac{12.5}{100} = \dfrac{125}{1000}
Finally, simplify the fraction:
\dfrac{125}{1000} = \dfrac{1}{8}
Question 3: Write \dfrac{19}{40} as a decimal.
[2 marks]
Treat the fraction as a division and divide 19 by 40,
\;\;\;\;\;0\;0.\;\;4\;\;\;7\;\;\;5\\40\overline{\left)1{}^19.{}^{19}0{}^{30}0{}^{20}0\right.}
So,
\dfrac{19}{40}=0.475
Question 4: Write 0.712 as a fraction in its simplest form.
[2 marks]
Write this decimal as a fraction with 1 on the bottom:
0.712=\dfrac{0.712}{1}
Make the numbers whole by multiplying the top and bottom of the fraction by 1000:
\dfrac{0.712 \times 1000}{1 \times 1000}=\dfrac{712}{1000}
Finally, simplify the fraction fully:
\dfrac{712}{1000}=\dfrac{89}{125}
Question 5: Write the following in order from largest to smallest:
\dfrac{1}{2}Â Â Â Â Â \dfrac{13}{25}Â Â Â Â Â Â 0.51Â Â Â Â Â 51.2\%
[2 marks]
Convert all of the numbers into decimals:
\dfrac{1}{2} = 0.5
\dfrac{13}{25} = 0.52
51.2\% = 0.512
Rewrite the list as decimals:
0.5Â Â Â Â Â 0.52Â Â Â Â Â 0.51Â Â Â Â Â 0.512
Put the list in order from largest to smallest, using the technique of ordering decimals:
0.52Â Â Â Â Â 0.512Â Â Â Â Â 0.51Â Â Â Â Â 0.5
Write down the order, converting the decimals back into their original form:
\dfrac{13}{25}Â Â Â Â Â 51.2\%Â Â Â Â Â 0.51Â Â Â Â Â \dfrac{1}{2}
Question 6:Â Write the following in order from smallest to largest:
\dfrac{6}{10}Â Â Â Â Â 55\%Â Â Â Â Â 0.65Â Â Â Â Â \dfrac{14}{20}
[2 marks]
Convert all of the numbers into decimals:
\dfrac{6}{10}=0.6
55\%=0.55
\dfrac{14}{20}=0.7
Put these decimals in order:
0.55Â Â Â Â Â 0.6Â Â Â Â Â 0.65Â Â Â Â Â 0.7
Write down the order, converting the decimals back into their original form:
55\%Â Â Â Â Â \dfrac{6}{10}Â Â Â Â Â 0.65Â Â Â Â Â \dfrac{14}{20}
Question 7:Â Write 115\% as decimal.
[1 mark]
Divide by 100 and remove the \% sign:
115\% \div 100=1.15
Functional Skills: Fractions, Decimals and Percentages Worksheet and Example Questions
Fractions, Decimals and Percentages L1
FS Level 1NewOfficial PFS
Fractions, Decimals and Percentages L2
FS Level 2NewOfficial PFS[responsive-flipbook id=”pfs_pocket_revision_guide_-_sample”]
Revision Products
Functional Skills Maths Level 2 Pocket Revision Guide
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact revision guide.
Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.
Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.
Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.
Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.
