Functional Skills: Maps and Scale Drawings
Maps and Scale Drawings
Scale drawings are used to represent larger or smaller objects, drawings, images or maps.
There are 6 skills you need to learn for scale drawings.
Make sure you are happy with the following topics before continuing.
Skill 1: Understanding Scale Keys and Scale Factors
Scale factors are used to accurately scale up or down an image. Scale drawings will come with a key, or a scale factor, that tells you what a dimension in the drawing is equal to in real life.
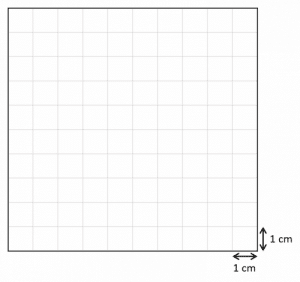
They are usually represented as ratios, with an = sign or as a line drawing, as seen on the 1 cm grid below.

Note: These all mean the same thing!
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Notes:
- You may be given a scale drawing with a grid background, which makes questions easy. If you are not given a grid background, then you will need to use a ruler to measure distances and line drawings.
- You may need to convert distances that you have been given in the question or distances that you have measured into a more sensible unit.
Skill 2: Calculating Distances by Measuring
Example: The scale drawing below shows a section of coastline. Calculate the distance between point A and point B.

We first need to measure the length of the scale, using a ruler. It is 1 cm long. Therefore 1 cm on the drawing represents 5 km in real life.
Then, measure the distance between A and B on the drawing, using a centimetre ruler:

Since 1 cm on the drawing represents 5 km in real life, the distance between A and B in real life is:
8.5 \times 5 = 42.5 km
Skill 3: Calculating Distances on a Grid
Example: Below is a map of Africa. Calculate the real-life distance between Dakar and Khartoum, marked on the map.
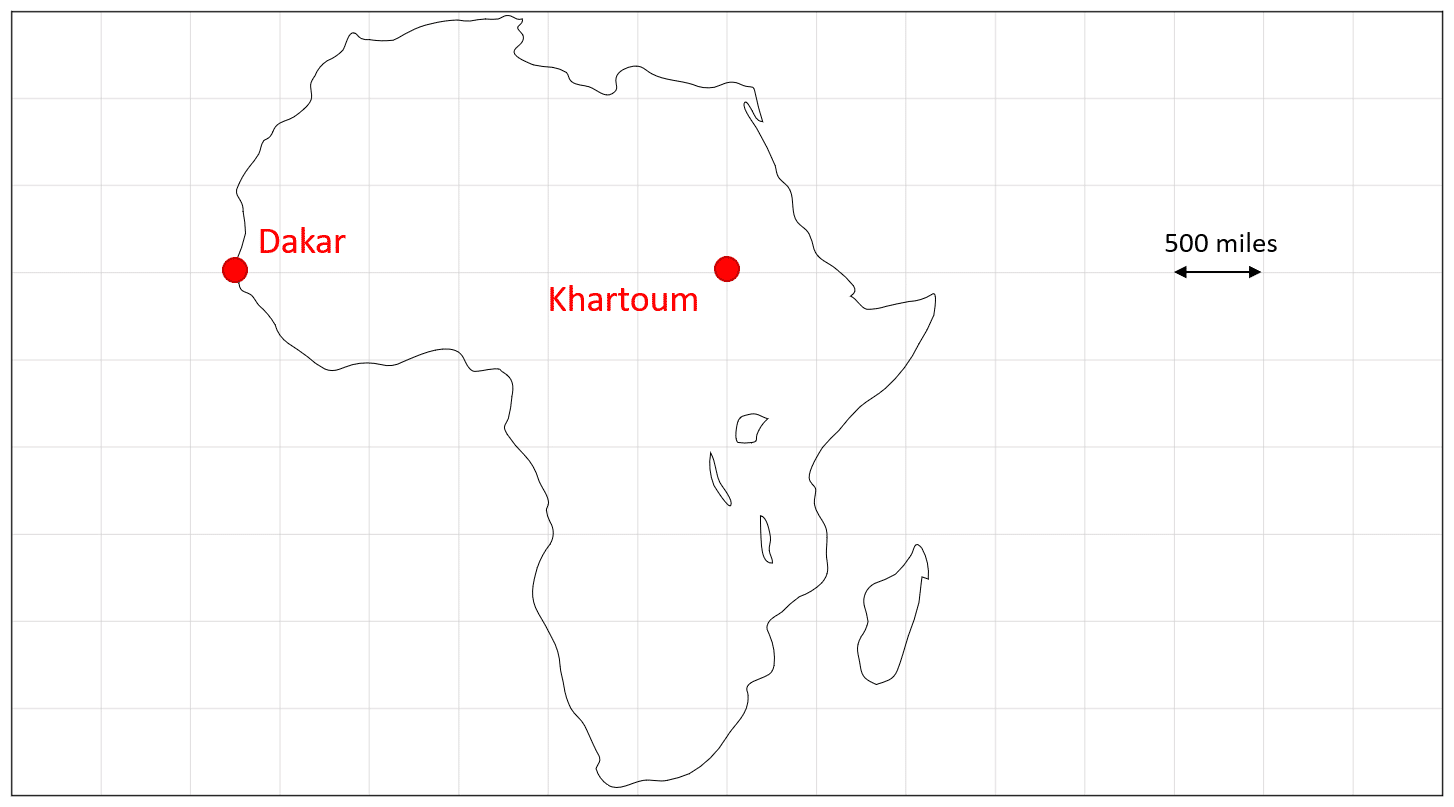
We are given the scale as a line drawing on a grid, so we do not need to use a ruler.
1 square on the grid is equal to 500 miles in real life
Count the number of squares between the two cities on the map:
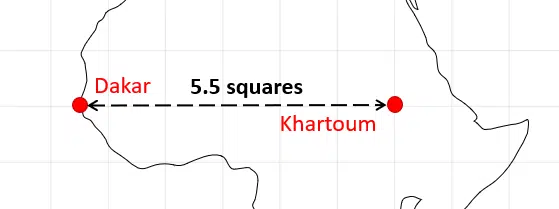
There are 5.5 squares between Dakar and Khartoum on the map.
To find the real-life distance between Dakar and Khartoum, multiply the distance represented by 1 square by the number of squares between the two cities:
5.5 \times 500 = 2750 miles
Skill 4: Working out the Scale
You may be asked to find the scale on a map or drawing, given a distance.
Example: The diagram below is a scale drawing of a classic car. The length of the car in real life is \textcolor{limegreen}{3.2} m.
Calculate the scale used in the drawing. Give your answer as a ratio.

We need to measure the length of the drawing, using a centimetre ruler:
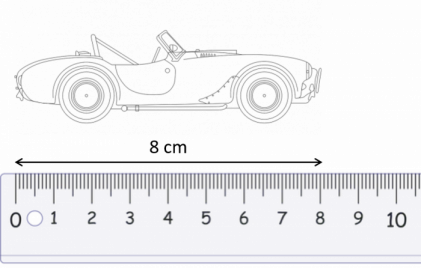
The length of the car is \textcolor{red}{8} cm on the drawing.
Both measurements need to be in the same units, so convert the length of the car in real life to cm:
Real-life length = \textcolor{limegreen}{3.2} m = \textcolor{limegreen}{320} cm
So, we can write this as a ratio:
Drawing length : Real-life length = \textcolor{red}{8} : \textcolor{limegreen}{320}
and then simplify the ratio by dividing both sides by 8:
\textcolor{red}{1} : \textcolor{limegreen}{40}
This means that 1 cm on the drawing represents 40 cm in real life.
Skill 5: Making Scale Drawings
To make a scale drawing, you will need to work out the dimensions first.
Example: Draw a rectangle, on the grid below, of height 2.5 m and width 3 m.
Use the scale 1:50. Each square is 1 cm by 1 cm.

The grid is in cm, so convert the dimensions of the rectangle in to cm:
\textcolor{red}{\text{real height} = 2.5 \times 100 = 250 \text{ cm}}
\textcolor{blue}{\text{real width} = 3 \times 100 = 300 \text{ cm}}
1:50 means that 1 cm on the grid represents 50 cm in real life.
Divide the real dimensions by 50 to find the dimensions of the scale drawing:
\textcolor{red}{\text{drawing height} = 250 \div 50 = 5 \text{ cm}}
\textcolor{blue}{\text{drawing width} = 300 \div 50 = 6 \text{ cm}}
Finally, we can draw the rectangle on the grid, of height \textcolor{red}{5 \text{ cm}} and width \textcolor{blue}{6 \text{ cm}}

Skill 6: Using Bearings and Maps Together
Sometimes you will need to use a map to describe the distance between two places and what direction one is in respect to the other.
To do this you will need to use a map scale and then measure the distance and bearing. Make sure you revise the Angles and Bearings page first.
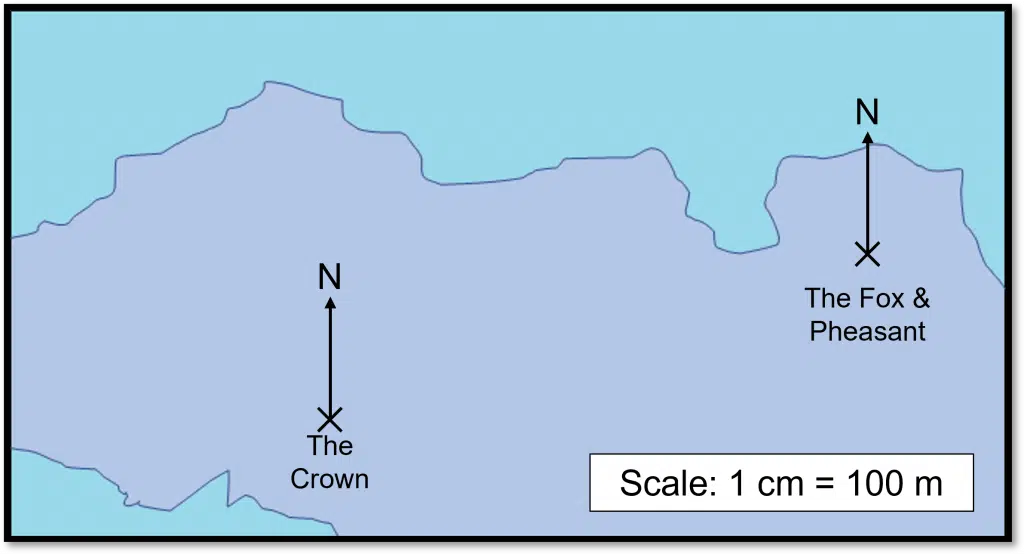

Example: The scale drawing shows part of a map for a town by the coast. It shows two pubs: The Crown and The Fox and Pheasant.
Describe the position of The Crown from The Fox and Pheasant.
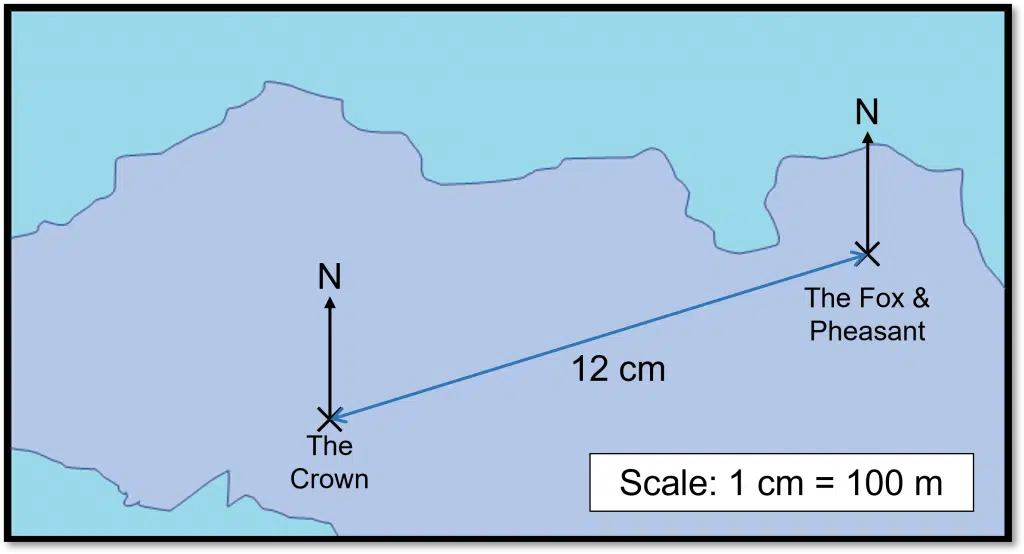

We first need to start with the distance between the two pubs. To do this draw a line between the two pubs and use a centimetre ruler to measure the length of the line. The length of this line will be different depending on the size of your screen, but if we take the line as being 12 cm long, then the distance between the two pubs is
12\times100=1200 m =1.2 km.
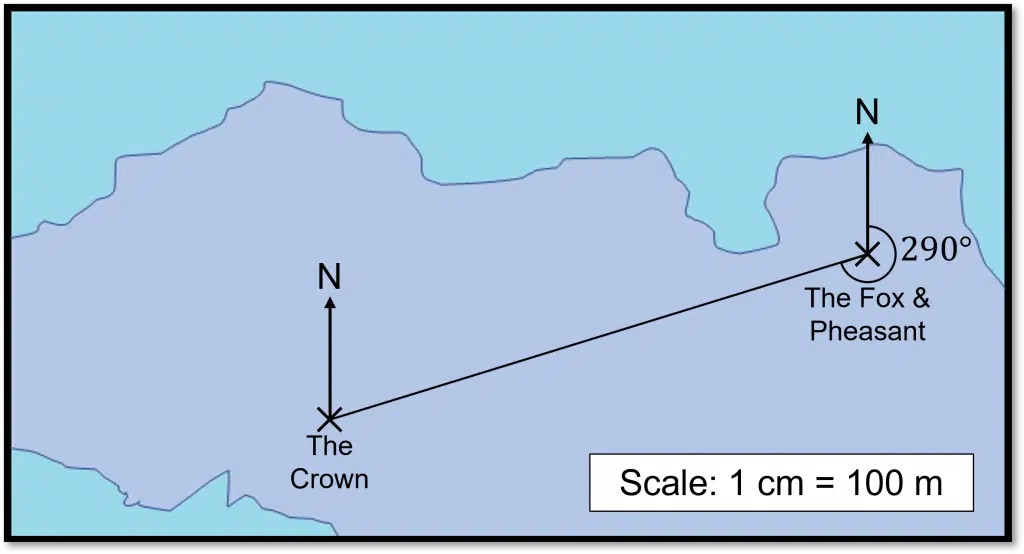

Finally, we need to measure the bearing. This is the clockwise angle from the North line.
The angle here is 290\degree.
Therefore, The Crown is 1200 m or 1.2 km from The Fox and Pheasant on a bearing of 290\degree.
Functional Skills: Maps and Scale Drawings Example Questions
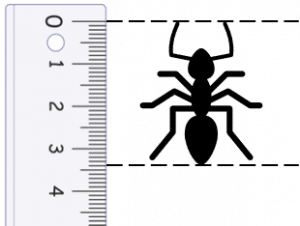
Question 1: The diagram below shows a scale drawing of an ant. The ruler shown is a centimetre ruler.
The drawing has a scale of 1:0.15
Calculate the length of the ant in real life. Give your answer in mm.
[2 marks]
1:0.15 means that 1 cm on the drawing represents 0.15 cm in real life.
In the drawing, the length of the ant is 3.4 cm.
Therefore, in real life the length of the ant is
3.4 \times 0.15 = 0.51 cm = 5.1 mm
Question 2: A section of a map is shown below. A and B are the locations of two hotels.
The scale of the map is 1 cm = 200 m.
The distance between the two hotels on the map is 3.9 cm.
Find the real-life distance between the two hotels.
[1 mark]
The distance on the map is 3.9 cm.
Each cm on the map represents 200 m in real life.
Therefore, the distance between the two hotels in real life is
3.9 \times 200 = 780 m
Question 3: In a town, the main shopping centre is situated 650 m away from the bus station. A map is drawn using the scale
1 cm = 250 m
Calculate the distance between the shopping centre and bus station on the map.
[1 mark]
Every 1 cm is equal to 250 m, therefore we need to divide 650 by 250 to find the distance between the shopping centre and bus station on the map:
650 \div 250 = 2.6 cm
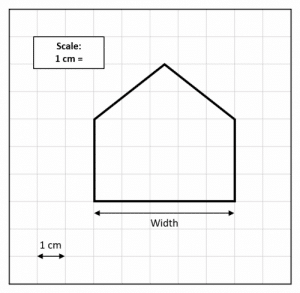
Question 4: The diagram below shows a scale drawing of a building that is 12 m wide.
Calculate the scale of the diagram. Give your answer as a ratio.
[2 marks]
The width of the house is 12 m in real life.
On the diagram, the width of the house 5 squares (5 cm) wide.
Convert both dimensions into the same units, so convert the width of the house in real life to cm:
12 \times 100 = 1200 cm
Therefore, the scale is
5 : 1200
This can be simplified by dividing by both sides by 5:
1 : 240
Question 5: A structure is in the shape of an isosceles triangle. The structure is 6 m wide and 8.5 m tall.
Draw a scale drawing of the structure on the grid below.
Use the scale 1:100
[3 marks]
Convert the real life dimensions to cm, so that all measurements are in the same units:
real life width = 6 \times 100 = 600 cm
real life height = 8.5 \times 100 = 850 cm
The scale 1:100 means that 1 cm on the grid represents 100 cm in real life.
So, divide the real life dimensions by 100 to find the dimensions of the scale drawing:
drawing width = 600 \div 100 = 6 cm
drawing height = 850 \div 100 = 8.5 cm
Finally, draw the scale drawing:
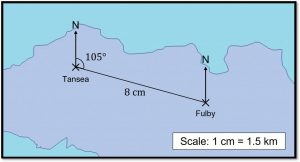
Question 6: Using the map below, describe the position of the town Fulby from the town Tansea.
[3 marks]
We first need to measure the distance between the two towns using a centimetre ruler. The distance may be different depending on the size of your screen, so don’t worry if you measure a different length.
We will then need to measure the the bearing, which is the clockwise angle from the North line.
The distance on our map is measured to be 8 cm, so the actual distance, using the scale, is 8\times1.5=12 km.
The bearing is 105\degree.
So we can say that Fulby is 12 km from Tansea on a bearing of 105\degree.
Specification Points Covered
L1.21 – Recognise and make use of simple scales on maps and drawings
L2.18 – Calculate actual dimensions from scale drawings and create a scale diagram given actual measurements
Functional Skills: Maps and Scale Drawings Worksheet and Example Questions
Maps and Scale Drawings L1
FS Level 1NewOfficial PFSMaps and Scale Drawings L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.