Functional Skills: Number Patterns
Functional Skills: Number Patterns Revision
Number Patterns
Number patterns are lists of numbers that follow a rule or a sequence.
The rule describes how you get from one number to the next.
Questions on number patterns might involve finding the rule, finding the next numbers in a sequence, or using this knowledge in a practical setting.
Types of Number Pattern
The number patterns that you will see in this course all follow the same type of rule – add or subtract the same amount to get to the next number.
Example:Â 1,\;4,\;7,\;10,\;13... has the rule +3 each time.
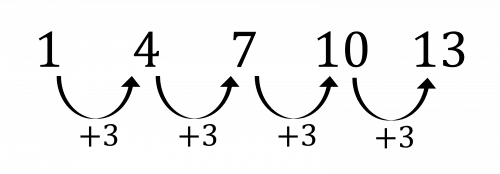
Example:Â 28,\;23,\;18,\;13... has the rule -5 each time.
Example:Â What is the rule of the sequence 84,\;59,\;34,\;9...?
It is decreasing so it is a subtracting rule.
84-59=25 so the rule is -25
Example:Â What comes next in the sequence 12,\;16,\;20,\;24...?
First, we find the rule. The sequence is increasing so it is an addition rule, and 116-112=4 so the rule is +4
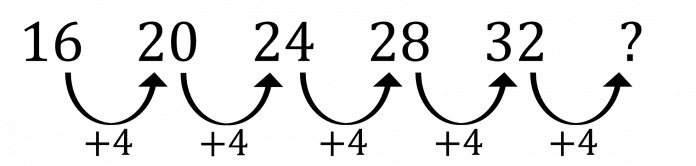
Now we apply the rule to the last number in the sequence.
32+4=36
So the next number in the sequence is 36
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Decimals in Number Patterns
Some number patterns contain decimal numbers. We use exactly the same methods that we do for whole number sequences.
Example:Â 0.8,\;1.1,\;1.4,\;1.7... has the rule +0.3
Example:Â 22.5,\;21.9,\;21.3,\;20.7... has the rule -0.6
Example:Â What is the rule of the sequence 9.9,\;8.7,\;7.5,\;6.3...?
The sequence is decreasing so it is a subtraction rule.
9.9-8.7=1.2 so the rule is -1.2
Example:Â What comes next in the sequence 3.1,\;3.5,\;3.9,\;4.3...?
First we find the rule. The sequence is increasing so it is an addition rule, and 3.5-3.1=0.4 so the rule is +0.4
Now we apply the rule to the last number in the sequence.
4.3+0.4=4.7
So the next number in the sequence is 4.7
Example 1: Whole Number Patterns
Find the rule and next term in these sequences:
a) 1,\;5,\;9,\;13...
b) 28,\;26,\;24,\;22...
[4 marks]
a) The sequence is increasing so it is an addition rule. 5-1=4 so the rule is +4
If we apply this rule to the last term we get 13+4=17, so 17 is the next term.
b) The sequence is decreasing so it is a subtraction rule. 28-26=2 so the rule is -2
If we apply this rule to the last term we get 22-2=20, so 20 is the next term.
Example 2: Decimal Number Patterns
Find the rule and next term in these sequences.
a) 20.4,\;20.9,\;21.4,\;21.9...
b) 19.5,\;18.7,\;17.9,\;17.1,\;16.3...
[4 marks]
a) The sequence is increasing so it is an addition rule. 20.9-20.4=0.5 so the rule is +0.5
Applying this to the last term in the sequence gives 21.9+0.5=22.4, so the next term is 22.4
b) The sequence is decreasing so it is a subtraction rule. 19.5-18.7=0.8 so the rule is -0.8
Applying this to the last term in the sequence gives 16.3-0.8=15.5, so the next term is 15.5
Functional Skills: Number Patterns Example Questions
Question 1:Â Find the rule for these sequences:
a) 1,\;3,\;5,\;7...
b) 0.8,\;0.6,\;0.4...
c) 40,\;33,\;26,\;19,\;12...
d) 10.4,\;10.1,\;9.8,\;9.5,\;9.2...
e) 34,\;51,\;68,\;85...
[5 marks]
a) The sequence is increasing, so we have an addition rule.
3-1=2 so the rule is +2
b) The sequence is decreasing, so we have a subtraction rule.
0.8-0.6=0.2 so the rule is -0.2
c) The sequence is decreasing, so we have a subtraction rule.
40-33=7 so the rule is -7
d) The sequence is decreasing, so we have a subtraction rule.
10.4-10.1=0.3 so the rule is -0.3
e) The sequence is increasing, so we have an addition rule.
51-34=17 so the rule is +17
Question 2:Â Find the next term in these sequences:
a) 0.1,\;0.5,\;0.9...
b) 17,\;13,\;9,\;5...
c) 21,\;34,\;47,\;60,\;73...
d) 11.94,\;11.85,\;11.76,\;11.67...
[8 marks]
a) The sequence is increasing, so we have an addition rule.
0.5-0.1=0.4 so the rule is +0.4
Applying this rule to the last term in the sequence: 0.9+0.4=1.3
So the next term in the sequence is 1.3
b) The sequence is decreasing, so we have a subtraction rule.
17-13=4 so the rule is -4
Applying this rule to the last term in the sequence: 5-4=1
So the next term in the sequence is 1
c) The sequence is increasing, so we have an addition rule.
34-21=13 so the rule is +13
Applying this rule to the last term in the sequence: 73+13=86
So the next term in the sequence is 86
d) The sequence is decreasing, so we have a subtraction rule.
11.94-11.85=0.09 so the rule is -0.09
Applying this rule to the last term in the sequence: 11.67-0.09=11.58
So the next term in the sequence is 11.58
Question 3:Â Clarissa buys the same number of books per month. In January, she had 20 books. In February, she had 23 books. In March, she had 26 books.
i) How many books does she buy each month?
ii) How many books will she have in April?
[4 marks]
i) This is just finding the rule for the sequence 20,\;23,\;26.... The sequence is increasing so it is an addition rule.
23-20=3, so the rule is +3. This means Clarissa buys 3 books every month.
ii) Here we just need to apply our rule to the number of books in March.
26+3=29, so Clarissa will have 29 books in April.
Question 4: Owen estimates that his watch’s second hand sale value is decreasing by £5 every year. If it was worth £62 in 2019 and £57 in 2020, how much was it worth in 2021?
[2 marks]
Here we are given the rule (-5) and some terms in the sequence (62,\;57). So we have to apply our rule to the last term in the sequence.
57-5=52 so the watch was worth £52 in 2021.
Question 5:Â The amount of time Jack’s laptop takes to boot up increases with the age of the laptop. When it was new it took 1 second; after 1 year it took 5 seconds; after 2 years it took 9 seconds, and so on. How long will it take to boot when the laptop is 4 years old?
[4 marks]
Here, we have to establish the rule, then apply it twice. We apply it twice because we are given the time after 2 years but want the time after 4 years, so need to go 2 years ahead.
The sequence is 1,\;5,\;9..., which is increasing, so we have an addition rule.
5-1=4 so the rule is +4
We need to apply this rule twice. Once gives 9+4=13 and twice gives 13+4=17, so the laptop will take 17 seconds to boot up when it is 4 years old.
Functional Skills: Number Patterns Worksheet and Example Questions
