Functional Skills: Fraction Basics
Functional Skills: Fraction Basics Revision
Fraction Basics
Fractions are for when things are divided into equal parts. They are written as a top number, then a horizontal line, then a bottom number, for example \dfrac{3}{4}, which then the same as 3 \div 4.
The top number shows the number of parts you are considering, while the bottom number shows the number of parts in total. For example, if Bob eats 1 slice of cake and the entire cake is 10 slices, he has eaten \dfrac{1}{10} of the cake.
Make sure you are happy with the following topics before continuing.
Some Common Fractions
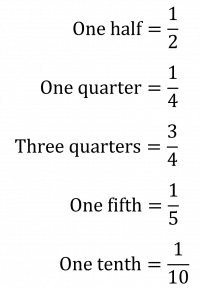
Fractions as Divisions
Fractions are also another way of writing divisions, for example \dfrac{2}{5}=2\div5
We can use this to turn fractions into decimals. All we do is type the division into the calculator.
\dfrac{2}{5}=2\div5=0.4
Here are our common fractions as decimals using this method:
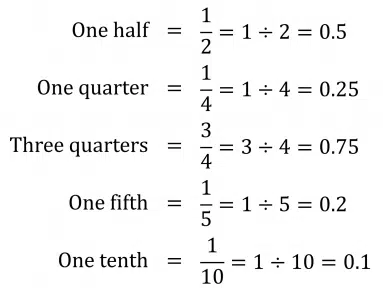
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Fractions of Something
If you are asked to calculate a fraction “of” an amount, you multiply the fraction by the amount.
Example:Â Find \dfrac{9}{10} of 40.
To do this, we do \dfrac{9}{10}\times40, which is equivalent to 9\div10\times40, which equals 36.
Equivalent Fractions
Equivalent fractions are fractions that have different numbers on the top and the bottom but represent the same value.
Example:Â \dfrac{1}{2} and \dfrac{2}{4} are equivalent, they have the same value.
\dfrac{1}{2}=1\div2=0.5
\dfrac{2}{4}=2\div4=0.5
Two fractions are equivalent if you multiply or divide the top and the bottom by the same number to get from one to the other.
Example:Â \dfrac{1}{5} is equivalent to \dfrac{3}{15} as we multiply both the top and the bottom by 3.
Example 1: Fractions of Something
Find the following:
a) \dfrac{1}{3} of 45
b) \dfrac{8}{10} of 75
c) \dfrac{2}{5} of 100
[3 marks]
a) \dfrac{1}{3}\times45=1\div3\times45=15
b) \dfrac{8}{10}\times 75=8\div 10\times 75=60
c) \dfrac{2}{5}\times100=2\div5\times100=40
Functional Skills: Fraction Basics Example Questions
Question 1:Â Write these fractions as decimals:
a) \dfrac{2}{5}
b) \dfrac{7}{10}
c) \dfrac{4}{5}
d) \dfrac{2}{3}
What is different about the answer to part d)?
[5 marks]
a) \dfrac{2}{5}=2\div5=0.4
b) \dfrac{7}{10}=7\div10=0.7
c) \dfrac{4}{5}=4\div 5=0.8
d) \dfrac{2}{3}=2\div 3 =0.6666...
The answer to part d) is different because it does not stop.
Question 2:Â Find the following:
a) \dfrac{2}{3} of 600
b) \dfrac{1}{3} of 36
c) \dfrac{3}{4} of 540
d) \dfrac{12}{5} of 290
[4 marks]
a) \dfrac{2}{3}\times600=2\div3\times600=400
b) \dfrac{1}{3}\times 36 =1\div 3\times36=12
c) \dfrac{3}{4}\times540=3\div4\times540=405
d) \dfrac{12}{5}\times 290=12\div5\times 290=696
Question 3:Â Are the following pairs of fractions equivalent?
a) \dfrac{1}{2} and \dfrac{3}{6}
b) \dfrac{1}{3} and \dfrac{3}{12}
c) \dfrac{2}{5} and \dfrac{24}{60}
d) \dfrac{3}{10} and \dfrac{6}{18}
e) \dfrac{2}{10} and \dfrac{5}{25}
[5 marks]
a) These are equivalent because we multiply the top and the bottom by 3 to go from \dfrac{1}{2} to \dfrac{3}{6}.
b) These are not equivalent because the top has been multiplied by 3 while the bottom has been multiplied by 4.
c) These are equivalent because we multiply the top and the bottom by 12 to go from \dfrac{2}{5} to \dfrac{12}{60}.
d) These are not equivalent because the top has been multiplied by 2 but the new bottom is 18 while 10\times2=20
e) There is no obvious multiplier for either top or bottom here, so to check we have to turn them into decimals.
\dfrac{2}{10}=2\div10=0.2 and \dfrac{5}{25}=5\div25=0.2, so they are the same, so they are equivalent.
Question 4:Â Which of these fractions is not equivalent to \dfrac{3}{5}?
\dfrac{12}{20},\dfrac{6}{10},\dfrac{24}{35},\dfrac{9}{15},\dfrac{150}{250}
[3 marks]
For \dfrac{12}{20}, both the top and the bottom have been multiplied by 4, so this is equivalent.
For \dfrac{6}{10}, both the top and the bottom have been multiplied by 2, so this is equivalent.
For \dfrac{24}{35}, the top has been multiplied by 8, but 5\times8=40 so the bottom has not been multiplied by 8. So, this is not equivalent.
For \dfrac{9}{15}, both the top and the bottom have been multiplied by 3, so this is equivalent.
For \dfrac{150}{250}, both the top and the bottom have been multiplied by 50, so this is equivalent.
Therefore, the only non-equivalent fraction is \dfrac{24}{35}.
Functional Skills: Fraction Basics Worksheet and Example Questions
