Functional Skills: Proportion
Functional Skills: Proportion Revision
Proportion
Two quantities are proportional if, as one changes, the other changes in a certain way.
We will explain direct proportion and inverse proportion.
Make sure you are happy with the following topics before continuing.
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Proportional Quantities
Example: Antonia has a recipe for a fruit drink shown below. She wants to make a big batch of this drink. Assuming the ingredients remain in proportion, calculate how much of the drink she makes if she uses 1100 ml of lemonade.
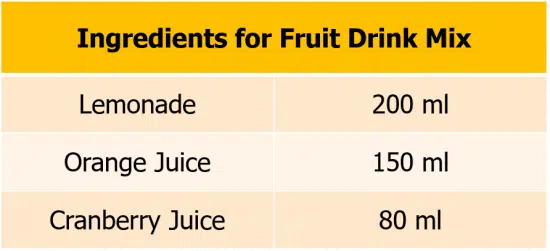
The ingredients remaining “in proportion” means that even after increasing their amounts, their ratio stays the same.
We need to determine by what scale factor the amount of lemonade has increased:
\textcolor{purple}{1100} \div 200 = \textcolor{limegreen}{5.5}
So, we can now calculate the amount of orange juice and cranberry juice used:
orange juice: 150 \times \textcolor{limegreen}{5.5} = 825 ml
cranberry juice: 80 \times \textcolor{limegreen}{5.5} = 440 ml
Therefore, the total amount the big batch of drink is:
1100 + 825 + 440 = \textcolor{black}{2365} ml
Note: This is an example of direct proportion.
Direct Proportion
Two quantities are directly proportional if as one increases, the other one increases at the same rate, e.g. as one is doubled, the other is doubled.
Example: Toni uses \textcolor{red}{150\text{ g}} of chocolate to make \textcolor{blue}{6} cookies. How much chocolate would Toni need to make \textcolor{purple}{20} cookies?
Step 1: Divide the amount of chocolate by 6 to find the amount needed for 1 cookie.
\textcolor{blue}{150} \div \textcolor{red}{6} = 25 g of chocolate
Step 2: Multiply the amount of chocolate needed for 1 cookie by the \textcolor{purple}{20} cookies needed.
\textcolor{purple}{20} \times 25 = 500 g of chocolate
Question - How do I improve my chances of passing the level 2 maths exam?
Answer – Subject knowledge assessment. This useful tool identifies the key areas of the exam you will need to work on in order to pass your level 2 exam for the first time.
Inverse Proportion
Two quantities are inversely proportional if as one increases, the other one decreases at the same rate, e.g. as one is doubled, the other is halved.
Example: It takes \textcolor{red}{8} workers \textcolor{blue}{25} months to build 10 houses. Assuming they all work at the same rate, how long would it take \textcolor{limegreen}{20} workers to build the same number of houses?
Step 1: Multiply the number of workers by the number of months, to find the time it would take 1 worker to build 10 houses:
\textcolor{red}{8} \times \textcolor{blue}{25} = 200 months
Step 2: Divide the time it takes 1 worker to build 10 houses by \textcolor{limegreen}{20} workers, to get the answer:
200 \div \textcolor{limegreen}{20} = \textcolor{black}{10} months
Notes:
When answering proportion questions, you need to assume that everything it done at the same rate, e.g. workers working at the same rate or someone running at the same rate.
Functional Skills: Proportion Example Questions
Question 1: Chantel is making tomato soup, using the ingredients in the recipe below:
4 tablespoons of butter
\dfrac{1}{2} of an onion
1 tin of tomatoes
400 ml of stock
This recipe makes 2 servings.
Work out how much of each ingredient Chantel would need to make 5 servings of tomato soup.
[2 marks]
Calculate the amount of each ingredient needed for 1 serving, by dividing the quantity of each ingredient by 2:
4 \div 2 = 2 tablespoons of butter
\dfrac{1}{2} \div 2 = \dfrac{1}{4} of an onion
1 \div 2 = \dfrac{1}{2} of a tin of tomatoes
400 \div 2 = 200 ml of stock
Then, multiply each quantity by 5, to find out how much of each ingredient is needed for 5 servings:
2 \times 5 = 10 tablespoons of butter
\dfrac{1}{4} \times 5 = \dfrac{5}{4} = 1 \dfrac{1}{4} onions
\dfrac{1}{2} \times 5 = \dfrac{5}{2} tins of tomatoes
200 \times 5 = 1000 ml of stock
Question 2: Aryna walks 4 km in 52 minutes. How long would it take her to walk 6 km?
Assume that she walks at the same rate.
[2 marks]
Divide 52 minutes by 4 to find the time it takes to walk 1 km:
52 \div 4 = 13 minutes
Then, multiply by 6 to find how long it would take to walk 6 km:
13 \times 6 = 78 minutes
Question 3: It takes 60 minutes for 3 gardeners to cut the grass of a field. Assuming they all work at the same rate, how long would it 5 gardeners to cut the same grass?
[2 marks]
Multiply 60 by 3 to find how long it would take 1 gardener to cut the grass:
60 \times 3 = 180 minutes
Then, divide by 5 to calculate how long it would take 5 people to cut the grass:
180 \div 5 = 36 minutes
Functional Skills: Proportion Worksheet and Example Questions
Proportion L1
FS Level 1NewOfficial PFS
Proportion L2
FS Level 2NewOfficial PFS[responsive-flipbook id=”pfs_pocket_revision_guide_-_sample”]
Revision Products
Functional Skills Maths Level 2 Pocket Revision Guide
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact revision guide.
Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.
Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.
Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.
Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.
