Functional Skills: Probability
Functional Skills: Probability Revision
Probability
Probability is a measurement of the likelihood of an event happening. We can use fractions, decimals and percentages to describe probabilities.
There are 4 skills you need to understand for probability.
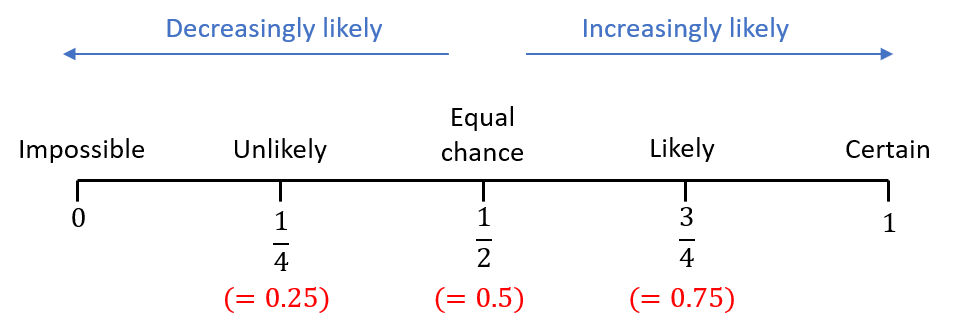
Skill 1: The Probability Scale
The probability scale summarises the likelihood of an event occurring:
- At the lower end of the scale, the likelihood of an event occurring is very small, so the probability is close to zero.
- As we move up the scale, events become increasingly likely.
- When the probability is \dfrac{1}{2}, there is an equal chance of an event occurring/not occurring.
- If the probability is less than \dfrac{1}{2}, the event is unlikely to occur.
- If the probability is greater than \dfrac{1}{2}, the event is likely to occur.
- Events that are impossible have a probability of 0 and events that are certain have a probability of 1
Notes:
- We usually express probabilities as fractions or decimals, but we can also use percentages. For example, a probability of \dfrac{1}{2} means there is a 50\% chance of the event occurring and a probability of \dfrac{3}{4} means there is a 75\% chance of an event occurring etc.
- You may sometimes see notation such as P(\text{event}) which means the probability of an event happening – the word in the bracket represents what the event is, e.g. you may see P(\text{odd}) which means the probability of something being odd, or P(\text{red}) which means the probability of something being red.
Follow Our Socials
Follow our Facebook for community support
Follow our Instagram & TikTok for revision help
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Follow our socials for revision tips and community support
Skill 2: Calculating Probabilities
We can calculate the probability of an event occurring if we know the total number number of possible outcomes.
Example:Â If we want to calculate the probability of rolling an even number on a standard die, we need the total number of possible outcomes. There are \textcolor{blue}{6} numbers on a standard die, of which \textcolor{red}{3} are even (2, 4 and 6). We can calculate the probability as follows:
Skill 3: Probabilities Add up to 1
All probabilities must add up to 1 (as decimals or fractions). So, we can calculate the probability of an event not happening by subtracting the probability that it will happen from 1:
Probability of event not happening = \, 1 \, - probability of event happening
Example: The probability of it raining tomorrow is \textcolor{red}{0.4}. What is the probability of it not raining tomorrow?
\begin{aligned} \text{Probability of no rain tomorrow} &= 1Â - \text{probability of rain tomorrow} \\ &= 1 - \textcolor{red}{0.4} = \textcolor{blue}{0.6} \end{aligned}
Skill 4: Events Happening Multiple Times
To find the probability of an event happening multiple times, we multiply the probabilities together.
Example: Mehmed has a coin. The probability of landing on tails is \textcolor{red}{0.5}.
Mehmed flips the coin three times. What is the probability of landing on tails on all three occasions?
\text{Probability of three tails} = \textcolor{red}{0.5} \times \textcolor{red}{0.5} \times \textcolor{red}{0.5} = \textcolor{blue}{0.125}
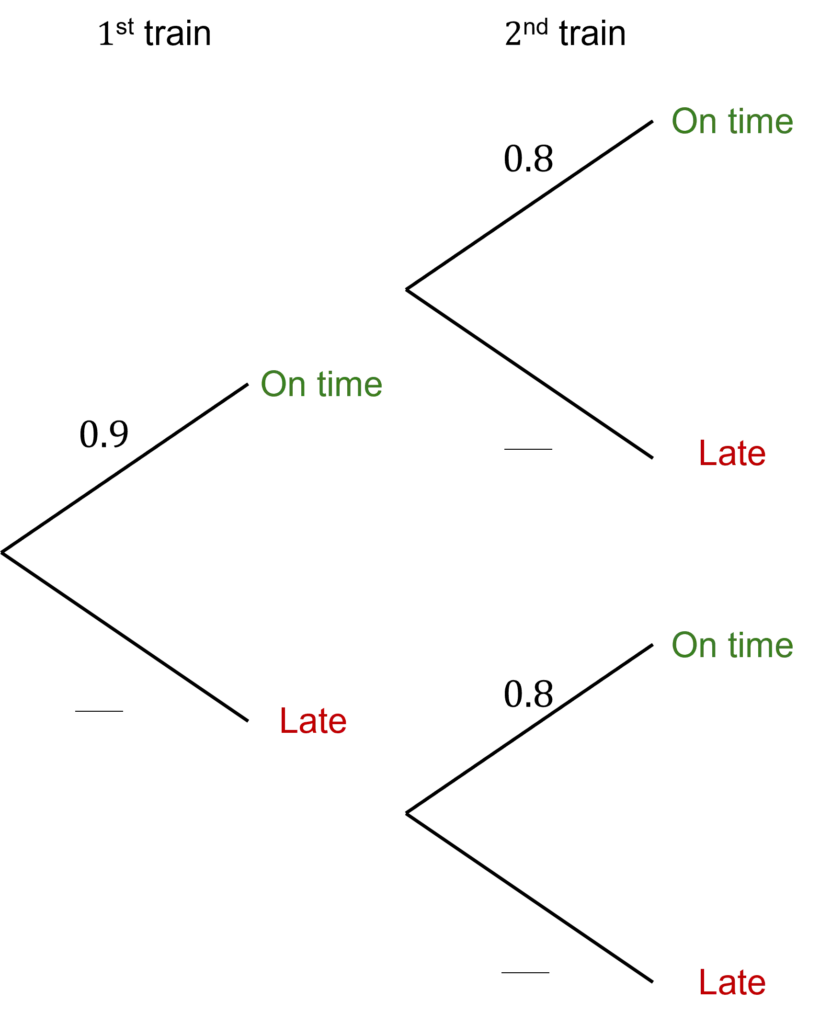
Skill 5: Probability Tree Diagrams
The probabilities of multiple events occurring can be represented on a probability tree diagram, as shown on the right.
The probability for each outcome is shown on each corresponding branch.
Example:Â Beth needs to catch two trains to get to work.
The probability that the first train is on time is 0.9 and the probability that the second train is on time is 0.8
Whether or not the first train is on time or late does not affect the probability that the second train is on time or late.
Complete the probability tree diagram and calculate the probability that both trains are on time.
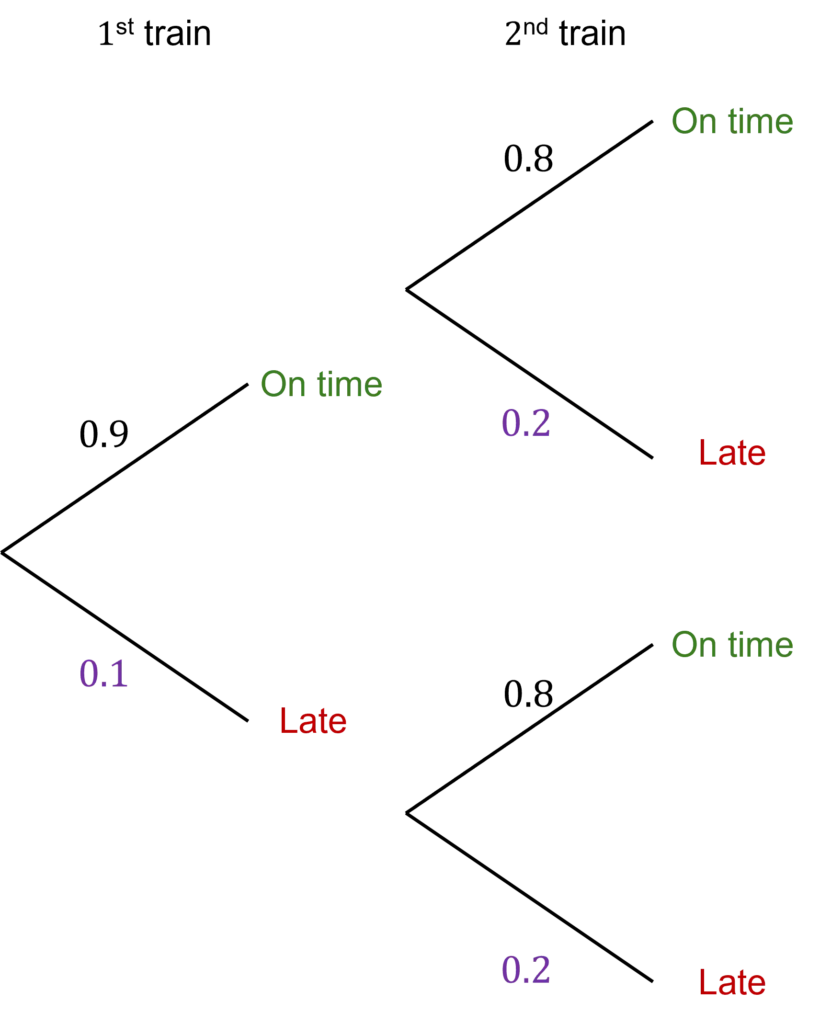
Step 1: Complete the probability tree diagram.
As stated in Skill 3, probabilities of all outcomes in a single event must add up to \bf{\textcolor{#f95d27}{1}}
Therefore, the probability that the first train is late is
1-0.9=0.1
Similarly, the probability that the second train is late is
1-0.8=0.2
Step 2: Calculate the probability of both trains being on time.
As stated in Skill 4, to find the probability of multiple events occurring we multiply the probabilities together.
So in this case, we multiply the probability of the first train being on time by the probability of the second train being on time:
0.9\times0.8=0.72Example: Probability Scale
Match up the following events with the labels on the probability scale.
i) The probability that it rains in any given week in winter
ii) The probability of getting ‘tails’ on a coin toss
iii) The probability that you will have a birthday this year
iv) The probability that you win the lottery
[4 marks]
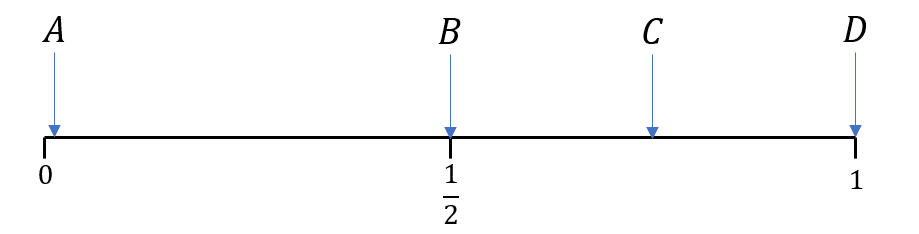
i) In any given week in winter, it is fairly likely (but not certain) that it will rain. The probability that it rains in any given week in winter will therefore be between \dfrac{1}{2} and 1, which matches up to \color{black}C
ii) The probability of getting tails on a coin toss is \dfrac{1}{2}, as there is an equal chance of getting heads or tails. This matches up to \color{black}B on the probability scale
iii) It is certain you will have a birthday each year (unless you are born on the 29th February in a leap year!), so the probability is 1, which matches up to \color{black}D
iv) The likelihood that you win the lottery is extremely small (but not impossible) so it will be very close to 0. This matches up to \color{black}{A}
Functional Skills: Probability Example Questions
Question 1: There are 250 employees in a business. The owner of the business is going to choose 20 employees at random to receive a bonus.
What is the probability of receiving a bonus? Give your answer as a percentage.
[2 marks]
Question 2: A box contains red and blue counters. The probability of picking a red counter out of the box is 0.35
What is the probability of picking a blue counter out of the bag?
[2 marks]
Probability of blue counter = 1 \, - probability of red counter = 1 - 0.35 = 0.65
Question 3: Jerry has a standard die. He rolls the die three times.
What is the probability of rolling a number 3 on all three occasions?
Give your answer as a fraction.
[2 marks]
The probability of rolling the a number 3 is \dfrac{1}{6}, since a die has 6 sides.
Therefore, to find the probability of rolling a number 3 on all three occasions, we multiply the probability of rolling a 3 by itself and then by itself again:
Probability = \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{216}
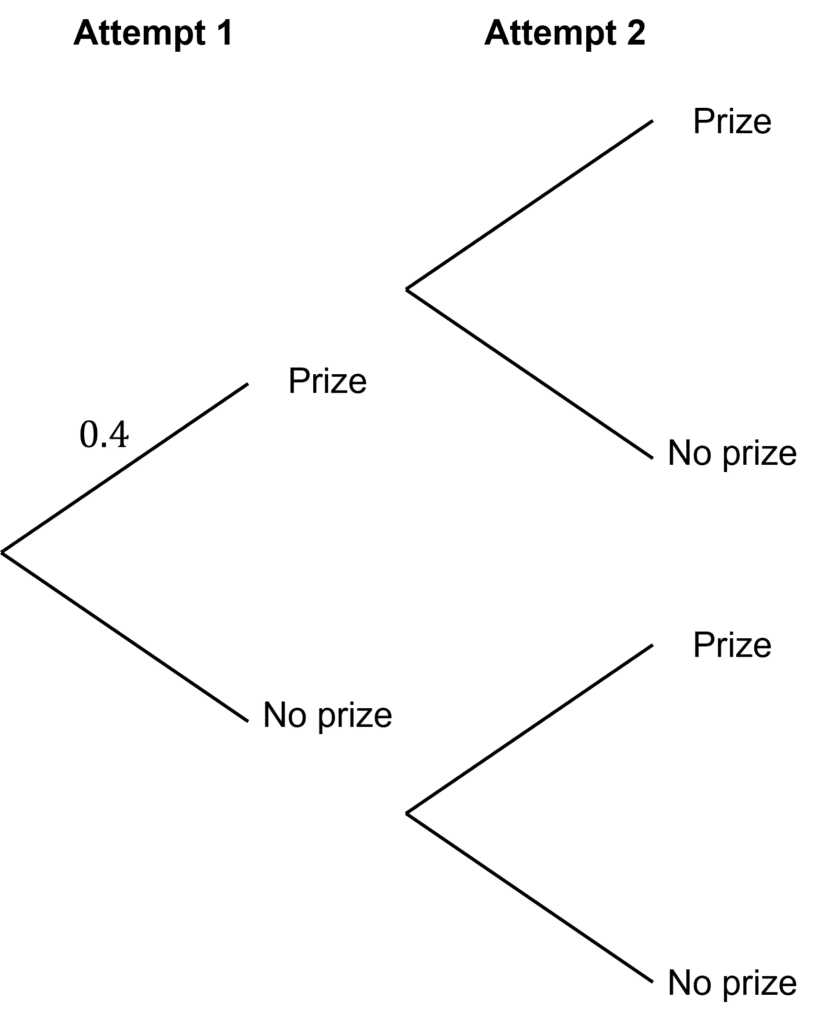
Question 4: Lois is playing a game at a fair.
The probability that she wins a prize is 0.4
The probability that she wins a prize is always the same.
She plays the game twice.
(a) Complete the probability tree diagram.
b) Work out the probability that she doesn’t win a prize after playing twice.
[4 marks]
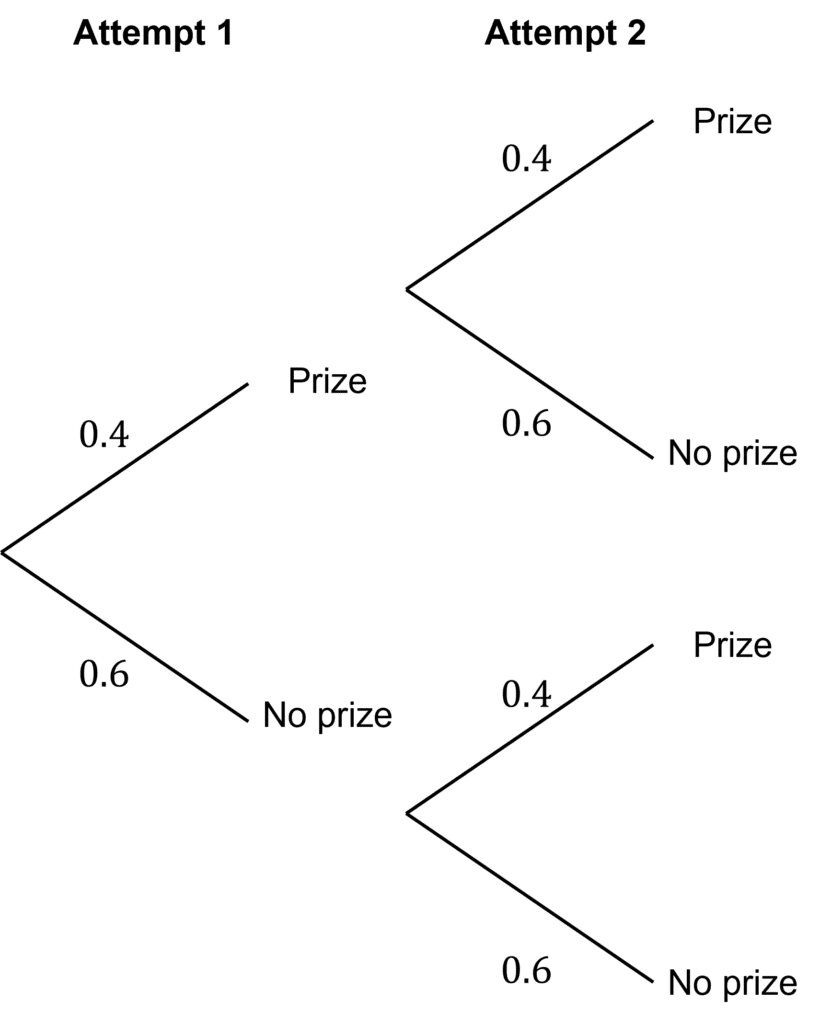
a) The probability that Lois doesn’t win a prize is
1-0.4=0.6
Here is the completed probability tree diagram:
b) The probability that Lois doesn’t win a prize on either attempt is
0.6\times0.6=0.36Functional Skills: Probability Worksheet and Example Questions
Probability L1
FS Level 1NewOfficial PFS
Probability L2
FS Level 2NewOfficial PFS[responsive-flipbook id=”pfs_pocket_revision_guide_-_sample”]
Revision Products
Functional Skills Maths Level 2 Pocket Revision Guide
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact revision guide.
Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.
Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.
Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.
Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.
