Functional Skills: Estimating the Mean
Estimating the Mean
We are often presented with grouped data in the form of a grouped frequency table. In this instance, we are not dealing with exact values so we can only estimate a value of the mean.
Make sure you are happy with the following topics before continuing.
Grouped Frequency Tables
Grouped frequency tables are a useful way of displaying broad data by grouping data into classes.
Example: the grouped frequency table below shows the number of exercise sessions attended by a group of people.
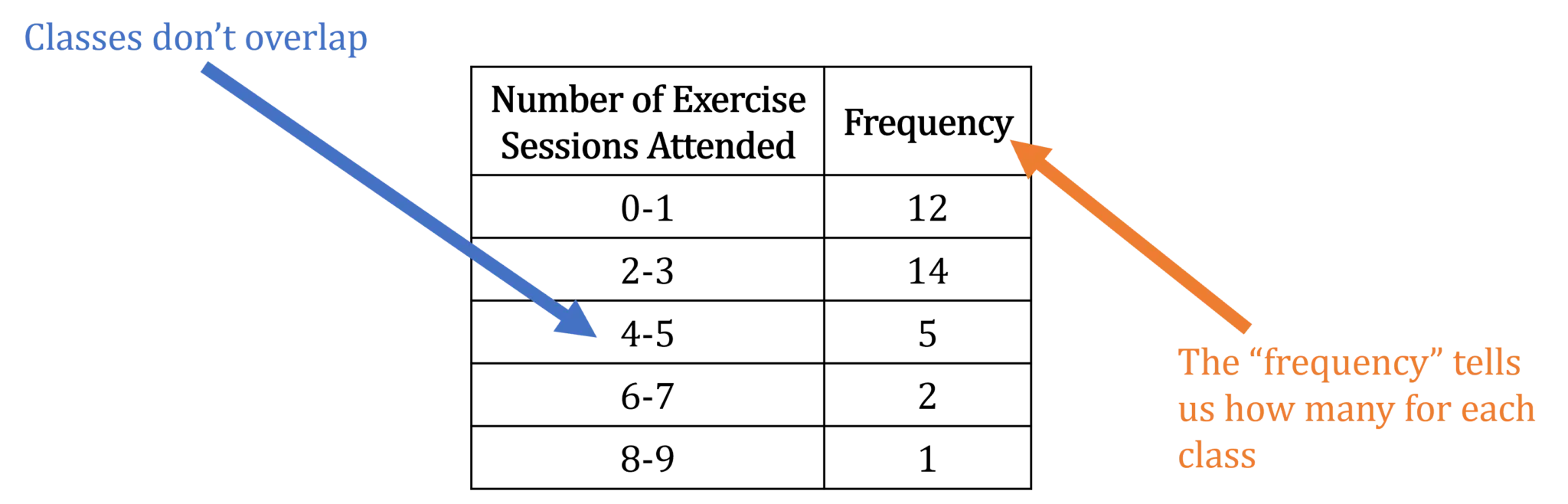
Note that the classes cannot overlap in a grouped frequency table – be careful when constructing grouped frequency tables not to put the same numbers in twice. For example, if the second class in the example above were 1-2, someone who attended 1 exercise session would fit into the first and second class.
In this example, all of the data is known but you may encounter other examples where the last class might say something like ‘10 or more’. This would also be useful if the data at the higher end was very spread out.
Estimating the Mean
We can use data from grouped frequency tables to estimate the mean value. The reason we are ‘estimating’ is because we do not know how the data is distributed in each class – it could all be at the lower end of the class, all at the higher end or evenly distributed throughout.
We estimate the mean by finding the midpoint of each class and assuming the midpoint to be an average value of each class. We then multiply the midpoint by the frequency, entering the values into a new column.

We can now estimate the mean by taking the total of the Midpoint \times Frequency column and dividing it by the total of the frequency column.
Mean = 85 \div 34 = 2.5
So the mean number of exercise sessions attended is 2.5
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Functional Skills: Estimating the Mean Example Questions
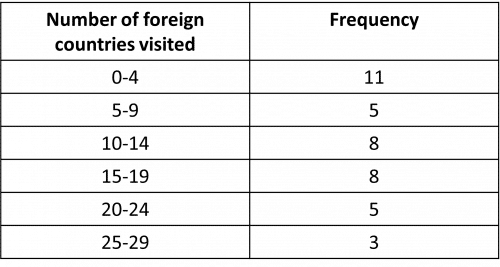
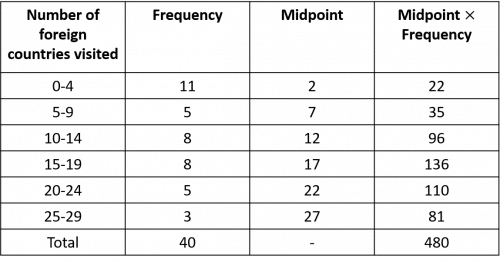
Question 1: 40 students were asked how many foreign countries they had visited. Their answers are displayed in the grouped frequency table below.
Estimate the mean number of foreign countries visited.
[4 marks]
First, fill out a new column with the midpoint of each class, then add a new column for the midpoint \times frequency.
The mean is:
480\div40=12 countries
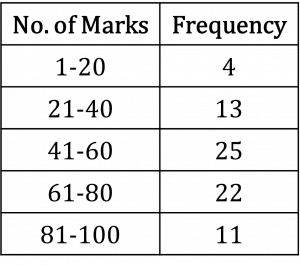
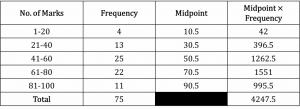
Question 2: A group of students took a maths test. Their scores are shown in the table below.
Estimate the mean test score.
[4 marks]
Fill out the midpoint and midpoint \times frequency column. Be careful with the midpoints – they must be exact so in this case we need to use decimals.
We can the estimate the mean as follows:
Mean = \dfrac{4247.5}{75} = 56.6333.... marks
If we want to give our answer to a whole number, we can round the mean to 57 marks.
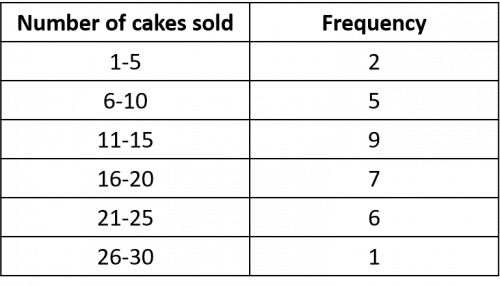
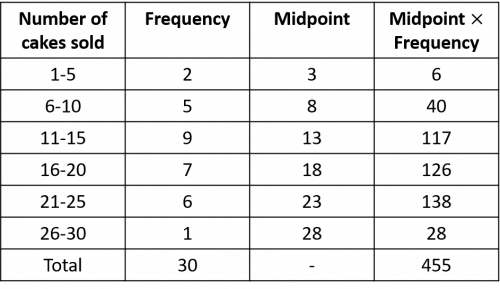
Question 3: A bakery records the number of cakes it sells each day for a month. Their sales data is shown in the table below.
Estimate the mean number of cakes sold in a day.
[4 marks]
Fill out a new column for the midpoint and the midpoint \times frequency. Next, find the total of the frequency column and the midpoint \times frequency column:
We can estimate the mean as follows:
Mean =\dfrac{455}{30}=15.166...
Rounding the answer to a whole number gives a mean value of 15 cakes sold per day.
Specification Points Covered
L2.24 – Estimate the mean of a grouped frequency distribution from discrete data
Functional Skills: Estimating the Mean Worksheet and Example Questions
Estimating the Mean L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.