Functional Skills: Comparing Data Sets
Comparing Data Sets
Averages and ranges can be used to compare different sets of data.
There are 2 skills that you need to learn for comparing data sets.
Make sure you are happy with the following topics before continuing.
Skill 1: Comparing Data Sets with Averages
When we want to compare two similar sets of data, there are a few things to consider.
Example: the table below displays the sales data from a car dealership across two consecutive weeks.
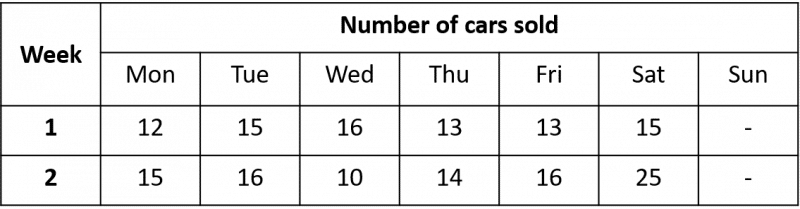
If we want to compare the sales data across the two weeks, we might want to consider the average (mean) number of cars sold each day.
The mean for Week 1 is: \dfrac{12+15+16+13+13+15}{6}=14
The mean for Week 2 is: \dfrac{15+16+10+14+16+25}{6}=16
So the mean number of cars sold per day was higher in Week 2. Usually we use the mean to compare two sets of data, as it takes all of the data into account. However, it is important to note that the mean is affected by outliers – data points which lie far away from the rest of the data. We can see that 25 cars were sold on the Saturday in Week 2 – this is much higher than the rest of the days in Week 2, so it increases the mean value significantly.
Instead of using the mean, you could compare the median or the mode for the two weeks. These averages are not affected by outliers, however they do not consider all of the data. There also may not be a mode if there are no repeated values.
Skill 2: Comparing Data Sets with the Range
The range is not a type of average, but it is still useful when comparing data. The range is the difference between the largest and smallest values in a data set, so it tells us how spread out the data is. If we consider the example of the car sales again,

The range for Week 1 is: 16-12=4
The range for Week 2 is: 25-10=15
The range is smaller for Week 1, so we can say the data is more consistent.
Follow Our Socials
Our Facebook page can put you in touch with other students of your course for revision and community support. Alternatively, you can find us on Instagram or TikTok where we're always sharing revision tips for all our courses.
Functional Skills: Comparing Data Sets Example Questions
Question 1: Two classes sat a maths test. Their marks are summarised in the table below.
Which class had a higher average mark?
[3 marks]
Use the mean to compare the average mark for each class.
The mean for Class 1 is: \dfrac{66+84+37+90+82+45+75+77+63+81}{10}=70
The mean for Class 2 is \dfrac{80+65+49+50+96+32+83+81+65+69}{10}=67
The mean is higher for Class 1 so we can say it had the higher average mark.
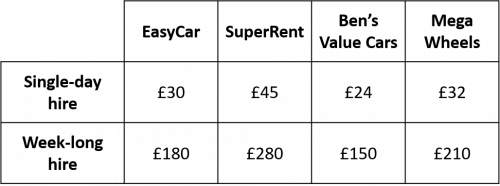
Question 2: Marvin wants to hire a car for his holiday. There are four car hire companies offering a range of prices, as shown in the table below.
a) Calculate the average cost of a single-day hire and a week-long hire.
b) Calculate the range in the costs of a single-day hire and a week-long hire.
[4 marks]
a) The average single day hire cost is:
\dfrac{30+45+24+32}{4}=£32.75
The average cost of a week-long hire is:
\dfrac{180+280+150+210}{4}=£205
b) The range in cost of a single-day hire is 45-24=£21
The range in cost of a week-long hire is 280-150=£130
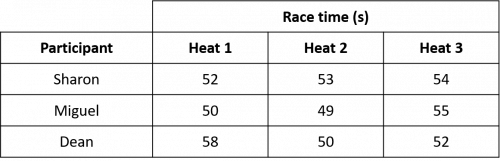
Question 3: Three athletes compete in a 400 m race. Their times for three heats are shown in the table below.
a) Who had the fastest average time across the three heats?
b) Who had the most consistent times across the three heats?
[4 marks]
a) Sharon’s average time is:
\dfrac{52+53+54}{3}=53 s
Miguel’s average time is:
\dfrac{50+49+55}{3}=51.33... s
Dean’s average time is:
\dfrac{58+50+52}{3}=53.33... s
So Miguel had the fastest average time.
b) The range in Sharon’s times is: 54-52=2 s
The range in Miguel’s times is: 55-49=6 s
The range in Dean’s times is: 58-50=8 s
So Sharon had the most consistent times and Dean had the least consistent times across the three heats.
Specification Points Covered
L2.23 – Calculate the median and mode of a set of quantities
L2.25 – Use the mean, median, mode and range to compare two sets of data
Functional Skills: Comparing Data Sets Worksheet and Example Questions
Comparing Data Sets L2
FS Level 2NewOfficial PFSRevision Products

Functional Skills Maths Level 2 Book
Revise and practice for your functional skills maths level 2 exam. All topics covered in this compact functional skills maths revision guide book.

Functional Skills Maths Level 2 Mini Tests
Practice for your functional skills Maths level 2, questions from every topic included.

Functional Skills Maths Level 2 Revision Cards
Revise for functional skills maths level 2 easily and whenever and wherever you need. Covering all the topics, with revision, questions and answers for every topic.

Functional Skills Maths Level 2 Practice Papers
This 5 set of Functional Skills Maths Level 2 practice papers are a great way to revise for your Functional Skills Maths Level 2 exam. These practice papers have been specially tailored to match the format, structure, and question types used by each of the main exam boards for functional skills Maths. Each of the 5 papers also comes with a comprehensive mark scheme, so you can see how well you did, and identify areas to improve on.

Functional Skills Maths Level 2 Practice Papers & Revision Cards
This great value bundle enables you to get 5 functional skills maths level 2 practice papers along with the increasingly popular flashcard set that covers the level 2 content in quick fire format.